Для нахождения этой вероятности используется биноминальный закон:
(14), где
n- число одинаковых элементов, входящих в систему;
m- число отказавших элементов;
Рn,m- вероятность того что из n элементов отражает m;
- число сочетаний из n по m;
q- вероятность отказа элемента.
Пример 5: Силовая установка самолета состоит из 3х двигателей. Вероятность отказа одного двигателя q=0,1 (условно). Самолет может совершать полет на двух двигателях. Требуется найти вероятность того, что полет будет происходить на двух двигателях.
Обозначим через Аi событие безотказной работы iго двигателя, через 
событие отказа iго двигателя, а через А событие отказа одного двигателя из трех.
Событие А может произойти при следующих комбинациях.
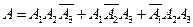
Применяя теоремы вероятность произведения и суммы независимых событий, найдем вероятность Р(А):
Вероятность того, что полет будет происходить на двух двигателях равна
1-0,243=0,757
Этот же результат получим, подставив в формулу (14)
Пример 6: Имеется 8 параллельно работающих гидроцилиндров. Вероятность отказа одного цилиндра q=0,1 (условно). Известно, что система сохраняет работоспособность при отказе четырех цилиндров. Требуется найти вероятность безотказной работы системы.
Подставив в формулу (14)
Вероятность безотказной работы системы равна 1-0,0046=0,9954
