Технология вычисления дисперсий группированных данных, примененная при решении задачи однофакторного дисперсионного анализа, может быть использована и для анализа более сложных производственных ситуаций. Рассмотрим, например, следующий типовой пример. Пусть на двух различных технологических установках производится выпуск одинаковых резисторов. Половину периода выпуска предприятие получает керамическую массу для производства резисторов от одного поставщика, а другую половину – от другого. Необходимо установить значимость различия средних значений механической прочности резисторов как между установками, так и между поставщиками при условии, что известные или неизвестные дисперсии параметра качества по отдельным изделиям одинаковы. Очевидно, что речь в данном случае идет о двухфакторном дисперсионном анализе.
Представим результаты контроля параметра качества в виде таблицы 6.2.
Таблица 6.2 Экспериментальные данные, полученные по двум установкам и двум поставщикам
| Установка 1 | Установка 2 | |
| Поставщик 1 | X11 X21 . I . . Xq1 | X12 X22 . II . . Xq2 |
| Поставщик 2 | X11 X21 . III . . Xq1 | X12 X22 . IV . . Xq2 |
Рассмотрим процедуру определения значимости различия средних по установкам (по столбцам таблицы 6.2).
1. Вычислить среднее значение 
(по первому столбцу), среднее значение 
(по второму столбцу) и общее среднее 
(по обоим столбцам).
2. Определить межстолбцовую дисперсию в соответствии с формулой:
. (6.85)
Здесь межстолбцовая сумма квадратических отклонений
. (6.86)
3. Найти внутригрупповую дисперсию 
. Из таблицы 2 видно, что число групп в эксперименте равно четырем. Для примера рассмотрим процедуру вычисления суммы квадратических отклонений по первой группе измерений, образованной отсчетами 
.
. (6.87)
Внутригрупповая сумма квадратических отклонений по всем четырем группам определяется по формуле
. (6.88)
4. Согласно формуле вычислить внутригрупповую дисперсию
. (6.89)
5. Согласно формуле вычислить статистику Фишера
(6.90)
и сравнить ее с критическим значением 
, определенным для интересующего пользователя уровня значимости. По результатам сравнения принять или отвергнуть гипотезу о значимости различия средних значений по установкам.
Рассмотрим процедуру определения значимости различия средних по поставщикам.
1. Вычислить среднее значение измерений в группах 
и группах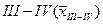 
.
2. Определить дисперсию между поставщиками по формуле
. (6.91)
Здесь сумма квадратических отклонений по поставщикам
. (6.92)
3. Вычислить статистику Фишера
(6.93)
и сравнить ее с критическим значением, найденным исходя из заданного уровня значимости.
Рассмотрим процедуру установление значимости эффектов взаимодействия. Под эффектами взаимодействия понимаются все эффекты, не объясняемые различием средних значений в столбцах, а так же различием средних между группами I-II и III-IV.
1. Вычислить сумму квадратических отклонений по всему объему эксперимента
. (6.94)
2. На основании,,,, вычислить сумму квадратических отклонений эффектов взаимодействия (
):
. (6.95)
3. Вычислить дисперсию взаимодействия по формуле
. (6.96)
4. Вычислить статистику Фишера
(6.97)
и сравнить ее с критическим значением, заданным исходя из необходимого уровня значимости.
В заключение отметим, что процедуры дисперсионного анализа реализованы в настоящее время в нескольких программных продуктах статистического анализа данных. В частности эти процедуры имеются в пакете анализа системы Excel.
