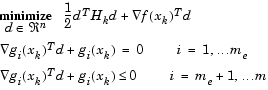
| (3-27) |
Данная подзадача может быть решена посредством применения алгоритма QP (см., например, раздел Решение квадратичного программирования). Такое решение основано на формировании новой итерации следующего вида
Параметр при длине шага 
определяется из соответствующей процедуры линейного поиска, которая обеспечивает приемлемое уменьшение получаемой функции выгоды (см. раздел Корректировка матрицы Гессе). Матрица 
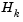является положительно определенной аппроксимацией матрицей Гессе для Лагранжевой функции. (уравнение 3-27). 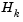может быть корректироваться посредством любого из квазиньютоновских методов, хотя метод BFGS (смотри раздел Корректировка матрицы Гессе), скорее всего, является наиболее популярным.
В отличие от решения методом SQP для задач без ограничений, нелинейные задачи при наличии ограничений решаются за некоторое число итераций. Одной из причин такого факта является то, что, вследствие наличия пределов на обозримые области, оптимизатор может принимать осознанные решения относительно направлений поиска и размера шага.
Рассмотрим функцию Розенброка (уравнение 3-2) при наличии дополнительных нелинейных ограничений в виде неравенств, g(x),
| (3-29) |
При применении метода SQP эта задача решается за 96 итераций по сравнению с 140 итерациями для задач без ограничений. На рисунке 3-6 представлен путь к точке решения 
начиная со стартовой точки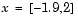 
.
