SQP метод является одним из самых современных методов в области нелинейного программирования. Шитковский [38], к примеру, успешно реализовал и провел тестовые расчеты по данной версии оптимизации и получил всестороннее превосходство, по сравнению с другими тестовыми методами, в части эффективности, точности и процента успешного решения задачи для большого числа тестовых задач.
Основанный на работах Бигса [1], Хана [24] и Пауэлла ([34], [35]) данный метод позволяет достаточно точно имитировать метод Ньютона для оптимизации при наличии ограничений, как это сделано для оптимизации без наличия ограничений. На каждой основной итерации осуществляется аппроксимация Гессиана для функций Лагнранжа при помощи квазиньютоновского модифицированного метода. Такой подход далее будет востребован для постановки подзадачи QP, решение которой далее уже используется для формирования направления поиска в процедуре линейного поиска. Обзор методов SQP можно найти в работах Флетчера [15], Гиль и др. [21], Пауэлла [37] и Шитковского [25]. Тем не менее, далее приводится описание обобщенного метода.
Согласно описанию задачу метода GP (уравнение 3-1) основная идея постановки подзадачи QP заключается в квадратичной аппроксимации функции Лагранжа.
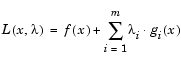
| (3-27) |
Последнее представляет собой упрощение уравнения 3-1 при предположении, что связанные ограничения могут быть представлены через ограничения в виде неравенств. Посредством линеаризации нелинейных ограничений можно получить подзадачу QP.






