В таблице 6.1 представлены экспериментальные данные, моделирующие результаты измерений, полученных в группах 
. Под группой 
здесь понимаются измерения, полученные для изделий, произведенных на первой установке, под группой 
- на второй и т.д.
Таблица 6.1 Экспериментальные данные, полученные по p группам
| N/N | F1 | F2 | … | Fp |
| . . . q | X11 X21 Xq1 | X12 X22 Xq2 | X1p X2p Xqp | |
| Групповая средняя |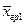 
| 
| 
|
Обозначим результат представленного в таблице произвольного измерения 
. Здесь индекс 
- номер измерения внутри группы, 
- номер группы. Предположим, что в статистическом смысле разница между группами отсутствует и любое представленное в таблице измерение получено из одной генеральной совокупности со средним значением 
и дисперсией 
. В этих условиях запишем дисперсию групповых (факторных) средних 
относительно общей средней по всей совокупности данных 
. (6.71)
Здесь
. (6.72)
Известно, что 
. С учетом этого из следует
. (6.73)
(Здесь дисперсии 
присвоено специальное обозначение 
, чтобы подчеркнуть, что она находится из групповой (факторной) дисперсии 
) Выражение в числителе последнего соотношения имеет смысл суммы квадратических отклонений групповых или иначе еще называемых факторных средних от общей средней. Введем для нее специальное обозначение
. (6.74)
С учетом этого обозначения соотношение может быть представлено в виде
. (6.75)
Здесь величина (p -1) имеет смысл числа степеней свободы, по которому определяется факторная дисперсия.
Далее запишем выражение для оценки j -й внутригрупповой дисперсии
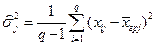. (6.76)
Усреднив эту оценку по всем p группам, находим
. (6.77)
(Здесь дисперсии присвоено специальное обозначение 
, чтобы подчеркнуть, что она находится из внутригрупповых дисперсий 
) Двойная сумма в числителе имеет смысл суммы квадратических отклонений внутригрупповых отсчетов от средних групповых значений. Назовем ее внутригрупповой суммой квадратических отклонений и обозначим
. (6.78)
С учетом этого обозначения соотношение может быть представлено в виде
. (6.79)
Здесь величина p(q-1) имеет смысл числа степеней свободы, по которому определяется внутригрупповая дисперсия.
И в заключение запишем выражение для оценки дисперсии по всей совокупности данных
. (6.80)
Двойная сумма в имеет смысл суммы квадратических отклонений всех отсчетов эксперимента от среднего значения эксперимента . Назовем ее общей суммой квадратических отклонений и обозначим
. (6.81)
В [1] показана справедливость важного равенства
. (6.82)
Поскольку первоначально было сделано предположение о статистической однородности всех измерений, три соотношения,, и являются оценками одной и той же генеральной дисперсии . Очевидно, что при увеличении объема измерительных данных в случае, если верна гипотеза о статистической однородности измерений, все три оценки дисперсий будут стремиться к одинаковому значению . Если же измерения в статистическом смысле неоднородны, например, в каждой группе (установке) значения генеральных средних 
различны, то все три оценки дисперсий, полученные по формулам, и, будут разными. Этот вывод и положен в основу однофакторного дисперсионного анализа. Для проверки гипотезы 
о статистической однородности измерений во всех группах против альтернативы 
о неоднородности измерений в группах вычисляется статистика F, имеющая распределение Фишера:
. (6.83)
Величины в числителе и знаменателе этой формулы (в числителе всегда должна стоять большая из дисперсий) вычисляются в соответствие с соотношениями и. Решающее правило для проверки гипотез имеет вид
(6.84)
Здесь 
- квантиль распределения Фишера уровня (1- 
) с (p -1) (числитель) и p (q -1) (знаменатель) степенями свободы.
Итак, процедура однофакторного дисперсионного анализа состоит в проверке гипотезы о том, что имеется одна группа однородных экспериментальных данных против альтернативы о том, что таких групп больше, чем одна. Под однородностью понимается одинаковость средних значений и дисперсий в любом подмножестве данных. При этом дисперсии могут быть как известны, так и неизвестны заранее. Если имеются основания полагать, что известная или неизвестная дисперсия измерений одинакова по всей совокупности данных, то задача однофакторного дисперсионного анализа сводится к исследованию значимости различия средних в группах данных.
