В данном разделе дается определение таких терминов, как базис, небазис и базисное допустимое решение для задачи линейного программирования. Для данных определений примем, что поставленная задача имеет следующий стандартный вид:
(Отметим, что A и b не являются некими матрицей или вектором, определяющими неравенства в исходной задаче). Предположим, что A есть матрица размерностью m -х- n с рангом m < n и соотвествующими колонками { a 1, a 2,..., a n}. Примем, что 
является пространством колонок A, с набором индексов B = { i 1, i 2,..., i m} и N = {1, 2,..., n}. N является дополнением B. Субматрица A B есть так называемый базис, а дополнительная субматрица A N есть так называмый небазис. x Bесть вектор базисных переменных и x N есть вектор небазисных переменных. При выполнении каждой итерации фазы 2 данного алгоритма производится замена одной колонки текущего базиса на колонку небазиса и, соответственно, корректируются переменные x B и x N.
Если х есть решение системы 
и все небазисные переменные для x N равны или их нижней или верхней границе, то х называется базисным решением.
Планирование второго порядка. Основные принципы, предпосылки и типы планов второго порядка.
Планы второго порядка. Ортогональное центральное композиционное планирование.
Одним из планов второго порядка является ортогональное центральное композиционное планирование (ОЦКП). Требование к составлению матрицы X, обеспечивающее диагональность матрицы С = ХT X, для ОЦКП сохраняется. В ортогональном центральном композиционном планировании к ядру, представляющему собой план ПФЭ 2n, добавляется центральная точка (хi= 0, i = 1, 2,…, n) и по две так называемые «звездные точки» для каждого фактора (хi = ±а, хi = 0 при j не равном i). При этом в каждой плоскости, проходящей через центр и содержащей ось Y и координатную ось i-го фактора, оказываются три значения фактора х, (-α, 0, +α) и три соответствующих значения Y. В результате общее число опытов в ОЦКП составит
N= 2n + 2n + 1, т.е. будет существенно меньше, чем, например, в плане ПФЭ 3n при n > 2.
Чтобы матрица второго порядка была ортогональной требуется выполнение условия
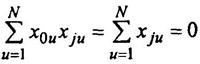(1)
для любых j ≠ 0, в частности, и для значений j, соответствующих квадратам факторов. В матрице планирования квадраты дают положительное число и их сумма в столбце не может равняться нулю. Чтобы удовлетворить условию выше, вводят преобразование квадратов факторов:
где а — постоянная, не зависящая от u.
Подставляя это преобразование в (1), получаем:
Из последнего выражения следует
И тогда преобразование квадратичных членов будет иметь вид
и условие диагональности для преобразованных квадратичных членов запишется в виде
Показано, что это условие будет выполнено при величинах звездного плана а, приведенных ниже:
Теперь можно дать матрицу планирования для ортогонального центрального композиционного планирования при n = 2. Рассматриваем аппроксимирующий полином
или с учетом преобразованных квадратичных членов
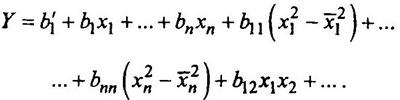
Если раскрыть скобки, то получим
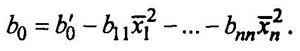
Сначала построим план ПФЭ 22. Коэффициенты вычисляются по формуле
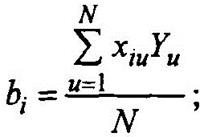
Таблица 5.1
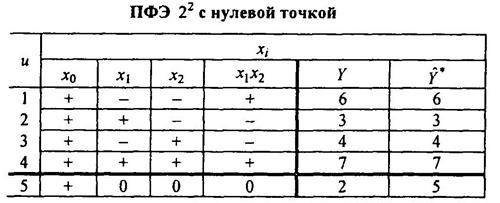
В результате:
Проверка близости Y и Y* в нулевой точке (см. пятую строку в матрице) |Y-Y*| =3 — аппроксимация очень грубая.
Переходим к плану второго порядка — ОЦКП. Для этого достроим план — к четырем опытам ПФЭ 22 добавим 2n = 4 опыта в «звездных» точках при а = 1 и еще опыт в нулевой точке (см. табл. 5.1, пятая строка), т.е. всего N=4+4+1=9.
В рассматриваемом примере
В результате матрица ортогонального центрального композиционного планирования, представленная в табл. 5.2, имеет вид.
Таблица 5.2
Матрица планирования ОЦКП
После вычисления коэффициентов получаем
или
Сравнение значений Y*, которые дал опыт, со значениями Y, полученными по аппроксимирующему полиному, показывает, что расхождение здесь много меньше.
