Одним из примеров системы из последовательно соединенных элементов является одна цепь линии электропередачи со всей защитной и коммутационной аппаратурой. Перерыв электроснабжения потребителя, питание
которого осуществляется по одноцепной линии электропередачи, наступает при отказе или повреждении любого из элементов: линии, выключателя, разъединителя и т.д. В общем случае, для системы, составляющей из n последовательно соединенных элементов с учетом свойства ординарности отказов электрооборудования, матрица вероятностей переходов имеет вид:

 (8.7)
(8.7)
Решение системы дифференциальных уравнений, получаемых при раскрытии приведенной матрицы, аналогично, как и в случае одноэлементной системы. Для исправного состояния системы в начальный момент времени:

 (8.8)
(8.8)
Считая, что в начальный момент времени система была неисправна, т.е.  и
и 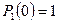 , получаем:
, получаем:

 (8.9)
(8.9)
Поскольку интенсивности отказов и восстановлений различны для разных элементов, составляющих данную систему, значения  и
и 
определяются по следующим выражениям:
 ;
;  (8.10)
(8.10)
Если система состоит из элементов, отказы которых являются зависимыми, порядок матрицы вероятностей переходов повышается. Предположим, что система состоит из двух последовательно соединенных элементов с одинаковыми параметрами потоков отказов и восстановлений, причем отказ второго элемента наступает только после отказа первого элемента и наоборот.
В этом случае система может находиться в трех состояниях: 0- рабочем, когда оба элемента исправны; 1- нерабочем, когда один из элементов поврежден; 2- нерабочем, когда отказали оба элемента. Граф переходов для такой системы приведен на рис. 8.1.
Рис. 8.1. Граф переходов для системы из двух последовательно соединенных элементов.
Вероятности переходов для возможных состояний системы определяются из следующих соображений:
1) если система в начальный момент времени находилась в 0-м состоянии, то она останется в этом состоянии при условии, что за интервал времени  ни один элемент не повредится. Эта вероятность составляет
ни один элемент не повредится. Эта вероятность составляет
 ,
,
т.к. вероятностью более одного перехода можно пренебречь.
2) за интервал времени  система перейдет из состояния 0 в состояние 1, если повредится хотя бы один элемент, а второй будет исправен. Вероятность этих событий определится как
система перейдет из состояния 0 в состояние 1, если повредится хотя бы один элемент, а второй будет исправен. Вероятность этих событий определится как  , где
, где 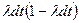 соответствует отказа первого элемента при исправном втором. Аналогично выражается вероятность отказа второго элемента при исправном первом элементе.
соответствует отказа первого элемента при исправном втором. Аналогично выражается вероятность отказа второго элемента при исправном первом элементе.
3) система переходит из состояния 0 в состояние 2, если за интервал  откажут оба элемента, что определяется выражением
откажут оба элемента, что определяется выражением  .
.
4) система переходит в состояние 1 из состояния 2, если за интервал  восстановится один из элементов. Вероятность этого события выражается как
восстановится один из элементов. Вероятность этого события выражается как 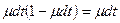
5) если система в начальный момент находилась в состоянии 1, за интервал  она возвратится в состояние 0 с вероятностью
она возвратится в состояние 0 с вероятностью  .
.
6) система останется в состоянии 1, если за интервал  поврежденный элемент не восстановился, а исправный не повредился. Эта вероятность равна
поврежденный элемент не восстановился, а исправный не повредился. Эта вероятность равна  .
.
7) из состояния 1 система переходит в состояние 2, если за время  поврежденный элемент не восстановился, а исправный повредился, что определяется как
поврежденный элемент не восстановился, а исправный повредился, что определяется как 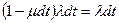 .
.
8) если в начальный момент система находилась в состоянии 2, то она перейдет в состояние 0, если за время  оба элемента восстанавливаются. Вероятность такого перехода равна
оба элемента восстанавливаются. Вероятность такого перехода равна 
9) за промежуток времени  система останется в состоянии 2, если за этот интервал даже один из элементов не восстановится. Вероятность этого состояния равна
система останется в состоянии 2, если за этот интервал даже один из элементов не восстановится. Вероятность этого состояния равна  .
.
Матрица вероятностей переходов для такой системы будет иметь вид:

 (8.11)
(8.11)
Система дифференциальных уравнений, описывающих процесс переходов, принимает вид:

 (8.12)
(8.12)

Дальнейшее решение системы уравнений (8.6) сводится к использованию прямых и обратных преобразований Лапласса с учетом исходных условий состояния системы. Однако, решение значительно упрощается, если рассматривать длительный период эксплуатации системы. В этом случае, как и при одноэлементной системе, вероятность нахождения системы в том или ином состоянии не зависит от начального момента рассмотрения процесса работы системы. Если к тому же принять, что события 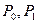 и
и 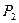 несовместимы, т.е. в одно и то же время может иметь место только одно из них, то можно считать, что
несовместимы, т.е. в одно и то же время может иметь место только одно из них, то можно считать, что 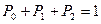 . Тогда система уравнений (8.6) преобразуется в следующую:
. Тогда система уравнений (8.6) преобразуется в следующую:
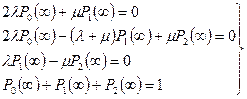 (8.13)
(8.13)
Решение этой системы относительно 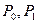 и
и 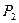 дает:
дает:

 ;
;  (8.14)
(8.14)
Следовательно, вероятность нахождения рассматриваемой системы в том или ином состоянии определяется параметрами потока отказов и восстановлений.




