Анализ и расчет надежности систем электроснабжения в конечном итоге сводится к оценке народнохозяйственного ущерба от перерывов электроснабжения. Именно этот показатель позволяет сделать заключение о приемлемости к практической реализации той или иной схемы, о необходимости дополнительных мероприятий с целью повышения надежности. Величина народнохозяйственного ущерба определяется длительностью перерыва электроснабжения, которая является зависимой от
интенсивности отказов оборудования и длительности восстановления его работоспособности.
Работа реальной системы электроснабжения не может рассматриваться как установившийся неизменный процесс, поскольку вследствие отказов и восстановления элементов система переходит из одного состояния в другое по мере того, как один или часть элементов повреждаются, а другие восстанавливаются.
Ранее отмечалось, что вероятности отказов и восстановлений элементов систем электроснабжения не зависят от начального момента рассмотрения процесса. Это означает, что вероятность появления перерыва электроснабжения определяется длительностью интервала между перерывами, но не начальным моментом времени. Системы подобного типа и процессы, происходящие в них, моделируются моделями, отражающими процессы Маркова и описываются уравнениями Маркова.
Рассмотрим одноэлементную систему, которая может находиться в двух состояниях: 0- безотказной работы, 1-состояние отказа (восстановления).
Задача сводится к определению вероятности нахождения системы в соответствующем состоянии в зависимости от начальных условий.
Исходной посылкой к решению задачи является условие, что поток отказов простейший с интенсивностью отказов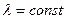 
и интенсивностью восстановлений 
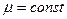, закон распределения времени между отказами и времени восстановления является экспоненциальным.
Опишем вероятности нахождения в различных состояниях в момент времени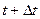 
1. Вероятность того, что система, находясь в начальный момент времени t в состоянии «0», за время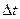 
не откажет, определяется как произведение вероятностей: вероятности нахождения системы в момент времени t в состоянии «0»- 
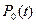и вероятности отсутствия отказа за интервал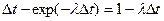 
В результате вероятность первой гипотезы равна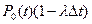 
.
2. Вероятность того, что система, находясь в начальный момент времени t в состоянии «1», за время 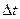восстановится и перейдет в состояние «0», также найдем по правилу перемножения вероятностей независимых событий: вероятности нахождения системы в момент времени t в состоянии «1»- 
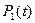и вероятности восстановления системы за интервал 
.
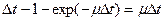Поэтому вероятность второй гипотезы равна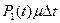 
.
3. Вероятность того, что система, находясь в момент времени t в состоянии «0», за интервал 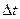откажет и перейдет в состояние «1» равна 
.
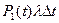4. Вероятность того, что система, находясь в момент времени t в состоянии «1», за интервал 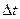не восстановится и останется в состоянии «1» равна 
.
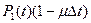Первые две гипотезы соответствуют рабочему состоянию системы, вторые две – состоянию отказа.
Вероятность рабочего состояния системы в момент времени 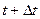определится как сумма вероятностей независимых событий:
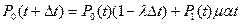(8.1)
Преобразовав это выражение, получим
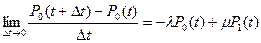(8.2)
или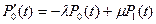 
Аналогично получаем вероятность нерабочего состояния системы
(8.3)
Изменение состояний можно проиллюстрировать с помощью графа
Для одноэлементной системы матрица вероятностей переходов имеет вид
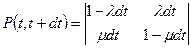
(8.4)
Рассмотрим решение дифференциальных уравнений при условии, что в начальный момент времени система находилась в состоянии «0», т.е.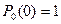 
, 
.
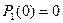Используя преобразования Лапласа, получаем систему уравнений
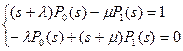(8.5)
где 
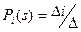(8.6)
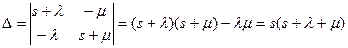
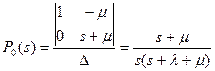
Обратным преобразование Лапласа получаем
и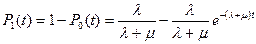 
Если исходить из условия 
и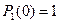 
, то будем иметь
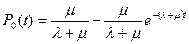
и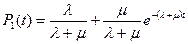 
Рассматривая достаточно продолжительный промежуток времени (в практических условиях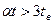 
), получаем
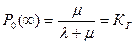- коэффициент готовности
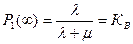- коэффициент вынужденного простоя.
