Реальные электрические сети представляют собой многочисленные сочетания последовательных, параллельных и смешанных соединений отдельных элементов. Рассмотрим возможность преобразования схемы, содержащей последовательно-параллельное соединение элементов. Предполагается, что пропускная способность элементов 2 и 3 равна 100%.
; 
;
; 
;
;
;
;
;
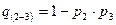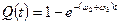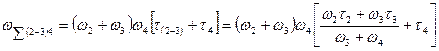Вероятность отказа параллельно соединенных элементов
(6.21)
Соответственно вероятность безотказной работы
(6.22)
Учитывая экспоненциальный закон распределения внезапных отказов
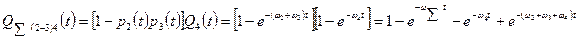
Дальнейшее преобразование схемы сводится к замене двух последовательно соединенных элементов единым эквивалентным.
Контрольные вопросы:
1. Показатели надежности системы из последовательно соединенных элементов.
2. Показатели надежности системы из параллельно соединенных элементов.
3. Показатели надежности при смешанном соединении элементов.
Учет плановых ремонтов при расчете надежности
При оценке надежности электроснабжения потребителя, когда питание его осуществляется от двух независимых источников (две цепи ЛЭП, два трансформатора, две подстанции и т.д.), необходимо учитывать возможность наложения аварии на плановый ремонт одного из источников. Исходными данными для расчета в этом случае должны явиться показатели надежности элементов 
и показатели плановых ремонтов 
.
Математическое ожидание числа наложений на плановый ремонт элемента 2 отказов элемента 1
(7.1)
где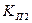 
- коэффициент планового простоя второго элемента.
Время одновременного простоя обоих элементов при наложении аварии на плановый простой зависит от соотношения времени планового простоя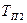 
и времени восстановления 
. Возможны следующие соотношения между этими величинами:
1) 
. В этом случае одновременный простой заканчивается с окончанием планового ремонта /Рис.7.1. а/.
Среднее время одновременного простоя, при условии равномерного распределения отказов в период планового простоя определяется по выражению
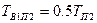(7.2)
2) 
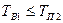. Для этих случаев длительность одновременного простоя ограничивается временем восстановления первого элемента (при отказах на интервале ) и временем окончания планового ремонта второго элемента, если отказ наступает на интервале 
/Рис.7.1. б), в) /. Во втором случае 
. Вероятность попадания отказа на интервалы времени 
и равны соответственно
и 
Среднее время одновременного простоя определится как
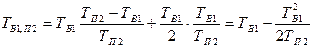(7.3)
Если длительность восстановления значительно меньше длительности планового ремонта, т.е. 
, то
(7.4)
Рис. 7.1. Средняя длительность одновременного простоя отказанного элемента (1) и находящегося в плановом ремонте элемента (2).
Коэффициент одновременного простоя обоих элементов вычисляется по формуле
(7.5)
В условиях эксплуатации для снижения возможного ущерба от перерывов электроснабжения плановые ремонты элементов проводятся в периоды с благополучными климатическими условиями. Данное обстоятельство учитывается введением поправочного коэффициента 
меньшего 1. Тогда, с учетом этого коэффициента
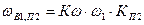(7.6)
Коэффициент планового простоя второго элемента
(7.7)
Контрольные вопросы:
1. Время одновременного вынужденного простоя вследствие наложения аварии на плановый простой при различных соотношениях времени восстановления и времени планового простоя.
2. Математическое ожидание числа наложений отказов одного элемента на плановый простой второго.
3. Коэффициент одновременного простоя, коэффициент планового простоя, коэффициент, учитывающий возможности смещения по времени плановых ремонтов.
