Статистическая обработка экспериментальных выборок выполняется в такой последовательности:
· исключить (или уменьшить) систематические составляющие погрешности из результатов наблюдений одним из известных способов: введения поправок, замещения, компенсации, противопоставления;
· проверить соответствие экспериментального закона распределения теоретическому, нормальному (аналитическим или графоаналитическим способом). Для случая, когда можно предполагать, что данная выборка является частью генеральной совокупности, распределенной по нормальному закону, обработка продолжается;
· вычислить наиболее вероятное значение 
искомой величины как среднее арифметическое выборки
· вычислить среднеквадратичное отклонение s результата наблюдения по формуле
или формуле Бесселя
или формуле Петерса для упрощенного вычисления с.к.о.
а для точных расчетов, учитывающих ограниченность числа опытов, по формуле
Значения коэффициента Mk приведены в литературе;
· при подозрении анормальности некоторого результата наблюдения xk, который заметно отличается от остальных в выборке, вычислить показатель анормальности для этого результата
После этого сопоставить значение показателя Vk с табличной величиной β для данного объема выборки и принятой вероятности γ. Если подозрения подтвердятся (критерием анормальности является условие Vk ³ β), этот результат наблюдения должен быть из выборки исключен, а значения и s вычислены заново (для этой же выборки, но без xk);
· вычислить коэффициент вариации v для данной выборки
v = 100 s/ , %;
· вычислить среднеквадратичное отклонение результата измерения
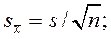
· вычислить доверительные границы ε случайной составляющей погрешности общего результата измерения
xн = - ε; xв = + ε,
где 
,
tγ - коэффициент доверия, значения которого приведены в зависимости от числа степеней свободы k = n – 1 и γ /4/,
γ - двусторонняя доверительная вероятность.
Обычно для технических расчетов вычисление доверительных границ производится с доверительной вероятностью равной γ = 0,95, в отдельных случаях, когда эксперимент невозможно повторить, принимают γ = 0,99 и только в особо ответственных случаях, когда результаты эксперимента влияют на жизнь и здоровье людей, допускается принимать γ = 0,999;
· вычислить доверительные границы общей погрешности результата измерения. Если доверительные границы неисключенных остатков систематической составляющей погрешности результата измерения близка к нулю, можно принять
Δ A» ε;
· записать результат прямого измерения в виде
x = A ± Δ A; γ = 0,95,
где А – наиболее вероятное значение результата измерения (A» );
Δ A – доверительная граница погрешности измерения.
Полная форма записи обязательна в том случае, если γ ¹ 0,95. При γ = 0,9 5 значение вероятности в записи результата измерения часто опускают.
· Следует отметить, что существует следующие три основные правила округления рассчитанного значения погрешности и полученного экспериментального результата измерения:
· погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной - если первая есть 3 и более;
· результат измерения округляется до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности;
· округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним-двумя лишними знаками.
