Приведенные выше основные положения теории погрешностей, исходные данные и расчетные формулы позволяют предложить следующий алгоритм обработки результатов многократных наблюдений при прямых и косвенных измерениях.
1. По правилам, приведенным в § 1.2, производится обнаружение, оценка и исключение систематических погрешностей из результатов наблюдений (т. е. исправление результатов наблюдений). Неисключенные систематические погрешности должны суммироваться со случайными при обработке результатов наблюдений. Но сначала все неисключенные систематические погрешности необходимо просуммировать между собой для оценки доверительных границ неисключенной систематической погрешности результата измерения Δс (см. § 1.3.1). При прямых измерениях и равномерном распределении неисключенных систематических погрешностей оценка Δс производится по формуле (ГОСТ 8.207—76):
, (1.38)
где Δci — граница (предел) i'-й неисключенной систематической погрешности; т — число суммируемых погрешностей, k — коэффициент, определяемый принятой доверительной вероятностью. При Р=0,95 k = 1,1, а при Р=0,99 k= 1,4.
Следует иметь в виду, что при m<4 значение Δс, вычисленное по формуле (1.38), может оказаться больше значения:
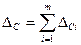, (1.39)
чего не может быть. Поэтому в качестве оценки границ неисключенной систематической погрешности результата измерения при m<4 нужно принять то из значений Δс, вычисленных по формулам (1.38) и (1.39), которое меньше.
Неисключенные систематические погрешности измерений Xi при косвенных измерениях можно оценить по формуле, аналогичной (1.31):
, (1.40)
а доверительные границы неисключенной систематической погрешности результата косвенного измерения — по формулам (1.38) или (1.39) при подстановке вместо Δс значений Δсxi, вычисленных по (1.40).
2. С помощью критериев, приведенных в § 1.3.1, проверяется принадлежность исправленных результатов наблюдений к нормальному распределению (или оно таковым принимается, как рекомендуется в § 1.3.2).
3. В случаях прямых равноточных измерений по формуле (1.17) рассчитывается значение 
, которое принимается за результат измерения. Для прямых неравноточных измерений таким образом вычисляются значения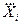 
, а при косвенных измерениях — значения , , 
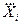и ν
4. По формуле (1.19) находятся случайные отклонения νi с помощью соотношения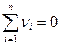 
проверяется правильность расчетов , , 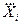и νi.
5. По формуле (1.20) вычисляются оценки 
, 
и 
С помощью критерия (1.23) или по ГОСТ 11.002—72 (в сомнительных случаях) проверяется наличие грубых погрешностей. Наблюдения, содержащие грубые погрешности, исключаются из ряда, и вычисления по пп. 3... 5 повторяются.
6. По формуле (1.21) вычисляются оценки , и В случае прямых неравноточных измерений по результатам вычислений с помощью формулы (1.26) определяются весовые коэффициенты αi, а с помощью формулы (1.27) — значение .
7. По формуле (1.24) для прямых неравноточных измерений или по формуле (1.29) для косвенных измерений рассчитываются значения или 
, которые принимают за результаты соответствующих измерений.
8. В случае косвенных измерений рассчитываются значения весовых коэффициентов 
по формуле (1.31) определяются частные погрешности 
. Если они не коррелированы, то по формуле (1.33) вычисляется значение 
. При коррелированных частных погрешностях либо по формуле (1.34) предварительно вычисляется оценка Rij и затем по формуле (1.30) рассчитывается искомое значение , либо для определения применяется методика с выделением групп частных погрешностей, сильно коррелированных между собой.
9. По заданной доверительной вероятности Р и числу наблюдений n определяется коэффициент Стьюдента t. Для прямых равноточных измерений его находят по табл. 1.2, а для прямых неравноточных измерений — после предварительного расчета числа степеней свободы по формуле (1.28). При косвенных измерениях прямое пользование табл. 1.2 правомерно для n>30. Если же n<30, то предварительно должно быть рассчитано по формуле (1.36) значение (п-1)эф. При дробных значениях (n-1) и (n-1)эф осуществляется интерполяция.
10. По формуле (1.22) для прямых измерений или по формуле (1.35) для косвенных измерений рассчитываются доверительные границы случайной погрешности результата измерения 
.
11. В случае прямых равноточных измерений ГОСТ 8.207—76 рекомендует далее вычислить отношение Δс/ .Если оно меньше 0,8, то значением Δс можно пренебречь по сравнению с и принять, что доверительные границы погрешности результата измерения = Δ.
Если же Δс/ >8, то пренебрегают значением по сравнению с Δc и принимают Δ=Δc. Если, наконец, эти неравенства не выполняются, значение Δ рекомендуется вычислять по формуле:
. (1.41)
Доказывается, что с погрешностью не более 10 % формула (1.41) заменяется более простой:
(1.42)
которая может считаться универсальной для всех рассматриваемых видов измерений.
12. Записывается окончательный результат измерений по одной из стандартных форм, приведенных в § 1.6.
