Математическое описание случайных погрешностей

 

Так как результаты наблюдений и случайные погрешности являются частным примером случайных величин, для математического описания их может быть использован аппарат теории вероятностей. Известно, что полностью свойства случайной величины описываются функцией распределения, определяемой как интегральная вероятность того, что случайная величина, например результат наблюдения Хi, будет меньше некоторого значения х:

 

Fx=P[Xi<x]. (1.6)

 

Функция fx, называемая также интегральной функцией (законом) распределения, является неубывающей функцией х, причем F(- )=0, a F() = 1. Веро­ятность попадания результата наблюдения в интервал [x1,x2] равна:

 

P[x1<Xi<x2]=FX(x2)-FX(x1)

 

Более наглядно свойства результатов наблюдений и случайных погрешностей описываются дифференциальной функцией (законом) распределения, называемой обычно плотностью вероятности:

 

(1.7)

 

При наличии ряда результатов наблюдений Х1, Х2,..., Хn график функции fx может быть построен по общеизвестному правилу при помощи гистограммы. С учетом отмеченных выше свойств можно показать, что

,

и

P[x1<Xi<x2] = 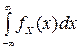(1.8)

 

В метрологической практике встречаются самые разнообразные функции распределения, причем не всегда их можно даже представить в аналитической форме. Тем не менее все многообразие реальных функций удается, как правило, аппроксимировать с удовлетворительной точностью стандартными аналитическими функциями, перечень которых в виде дифференциальных функций fΔст распределения абсо лютных погрешностей установлен ГОСТ 8.011—72 и приведен в табл. 1.1.

Из всех распределений, приведенных в табл. 1.1, наиболее часто при изучении случайных погрешностей встречается нормальное распределение. Центральная предельная теорема теории вероятностей утверждает, что реальное распределение случайных погрешностей будет близко к нормальному всякий раз результаты наблюдений формируются под влиянием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное воздействие по сравнению с суммарным воздействием всех остальных. Именно это характерно для большинства видов технических измерений. Нормальное распределение результатов наблюдений описывается дифференциальной функцией:

 

, (1.9)

 

где:

х — математическое ожидание (среднее значение) случайной величины Xi,

 

, (1.10)

 

где:

Dx — дисперсия, а σх — среднее квадратическое отклонение (СКО) результатов наблюдений Хi относительно тх.

 

 

Табл.1.1. Стандартные аппроксимации функций распределения

 

Фунция

График функции

f∆СТ

 

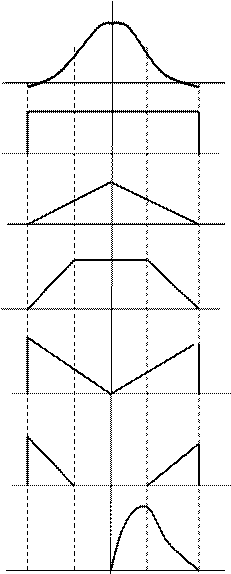
Нормальная (усеченная)

∆

 

Равномерная

 

∆

Треугольная (Симпсона)

 

Трапециевидная

 

	∆

Антимодальная 1

 

Антимодальная 2

 

 

Релея (усеченная)

На рис. 1.1 приведены графики fx, построенные по формуле (1.9) при σ’x>σx’’>σx’’’. Видно, что с ростом σx увеличивается рассеяние результатов наблюдений, т. е. вероятность появления больших погрешностей возрастает, а малых — уменьшается.

Для количественной оценки этой зависимости заменим в формуле (1.9):

 

(Xi-mX)/σX=t, (1.11)

 

и вычислим по формуле (1.8) вероятность попадания результата наблюдения в интервал[x1,x2]:

 

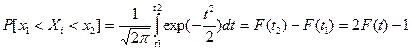. (1.12)

 

Функция F(t) табулирована и может использоваться для оценки случайных погрешностей. Однако при этом необходимо помнить, что точное определение значений тх и σх в формуле (1.11) возможно только при большом (теоретически бесконечном) числе наблюдений.

 

 

Xi

mX

 

Рис. 1.1. Графики нормального распределения при σ’x>σx’’>σx’’’.

 

Практически же число наблюдений всегда ограничено и при n<30 вместо распределения (1.9) необходимо пользоваться распределением Стьюдента:

 

(1.13)

 

где:

Г — гамма-функция.

При n>30 распределение (1.13) переходит в распределение (1.9) и является, таким образом, более универсальным. По аналогии с (1.12)

 

P[x1<Xi<x2]=2F(t,n)-1,

 

где:

F(t, n) — интегральная функция Стьюдента, значения которой также табулированы.

Хотя нормальное распределение встречается наиболее часто, каждый раз оценке случайных погрешностей должна предшествовать проверка принадлежности полученных результатов наблюдений к нормальному распределению. Правила такой проверки стандартизованы ГОСТ 11.006—74. Конкретно при n>50 проверка производится с использованием критериев Колмогорова (λn), Пирсона ( 2) или Мизеса — Смирнова (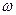 2). Если же 3<n<50, для проверки использу­ется специальный критерий (W).

Из других распределений, приведенных в табл. 1.1, отметим равномерное распределение, которое оказывается наиболее характерным для неисключенных систематических погрешностей. Хотя систематические погрешности являются детерминированными величинами (см. § 1.2), для разных условий измерений (например, повторные измерения в другой лаборатории, другими измерительными приборами и т. п.) такие составляющие, как неисключенные инструментальные погрешности и погрешности определения поправок, необходимо рассматривать и суммировать как случайные величины. Более того, если отсутствуют данные о виде распределения этих случайных величин, оно принимается равномерным, поскольку систематические погрешности оцениваются границами (пределами) допускаемых погрешностей, а не СКО, как это имеет место для случайных погрешностей.

В литературе неоднократно предпринимаются попытки предложить универсальную аналитическую функцию для описания всех симметричных распределений случайных погрешностей (табл.1.1). Это особенно актуально при применении ЭВМ для обработки результатов наблюдений. В качестве примера приведем дифференциальную функцию:

 

(1.14)

 

где:

— параметр, характеризующий крутизну спадов fx.

В частности, при α=1 распределение (1.14) экспоненциальное, при α= 2 оно совпадает c распределением (1.9), а при переходит в равномерное.

Функции распределения, являясь универсальным способом математического описания случайных погрешностей, не всегда удобны для практических целей и требуют предварительных тщательных экспериментальных исследований и обширных вычислительных работ. Поэтому в метрологической практике при оценке случайных погрешностей чаще ограничиваются использованием специальных числовых характеристик функций распределения, называемых моментами. Моменты представляют собой некоторые средние значения. Если усредняются величины, отсчитываемые от начала координат (рис. 1.1), моменты называются начальными, а если от центра функции распределения (табл. 1.1) — центральными. Так как результаты наблюдений и соответственно случайные погрешности являются дискретными случайными величинами, для определения начального момента k-го порядка необходимо пользоваться формулой

 

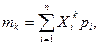(1.15)

 

а центрального момента k-го порядка

 

, (1.16)

 

где:

р — вероятность появления значения Xш.Если рассматривается полная группа событий, то , т.е. можно считать рi = 1/n.

Из начальных моментов чаще всего используется первый момент (k=1), который и является математическим ожиданием случайной величины Xi. Согласно (1.15),

 

. (1.17)

 

Из центральных моментов особенно важную роль играет второй момент (k=2)—дисперсия случайной величины Xi. Согласно (1.16) и (1.10),

 

. (1.18)

 

Находят также применение третий и четвертый центральные моменты.
В частности, параметр позволяет оценить симметричность функции распределения, а параметр , называемый эксцессом, характеризует островершинность ее. Для нормального распределения (1.9) s=0 и е=0. Поэтому нормальное распределение полностью характеризуется значениями mх и σх.

Заканчивая рассмотрение существующих приемов математического описания случайных погрешностей, подчеркнем еще раз, что для точного определения моментов необходимо большое (теоретически бесконечное) число наблюдений. Практически же число наблюдений, как уже отмечалось, всегда ограниченно, и чем сложнее эксперимент и выше его стоимость, тем оно меньше. Поэтому значения числовых характеристик функций распределения, найденные на основании ограниченного числа наблюдений, всегда приближенные и называются их точечными оценками. К точечным оценкам, обозначаемым в дальнейшем знаком «^», предъявляются требования состоятельности, несмещенности и эффективности. Состоятельной называют оценку, которая приближается (сходится по вероятности) к истинному значению оцениваемой величины при n . Несмещенной является оценка, математическое ожидание которой равно истинному значению оцениваемой величины. Наконец, эффективной будет та из нескольких возможных несмещенных оценок, для которой x = min.