Допустим, что имеется m групп независимых наблюдений одной и той же величины Q. По наблюдениям каждой группы вычислены средние арифметические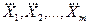 
и оценки СКО 
. За результат измерения в этом случае принимается оценка измеряемой величины по данным всех групп наблюдений. Она называется средним взвешенным и вычисляется по формуле:
, (1.24)
где коэффициенты αj отражают степень нашего доверия к оценкам 
и называются весовыми коэффициентами.
Так как систематические погрешности отсутствуют, то mxj-= mx= =Q, и из (1.24) следует:
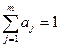(1.25)
В метрологической практике принято считать значения весовых коэффициентов обратно пропорционально дисперсиям групп наблюдений, т.е.
a1: a2:…: aj: …: av= 
Таким образом, с учетом (1.25):
(1.26)
Случайную погрешность результата измерения оценим, как и в случае равноточных измерений, значением:
,
которое при учете (1.26) может быть представлено в следующем окончательном виде:
. (1.27)
Доверительные границы случайной погрешности результата неравноточных измерений рассчитываются по формуле (1.22) с учетом данных табл. 1.2. При этом предварительно определяется число степеней свободы распределения Стьюдента по формуле:
. (1.28)
где n—число наблюдений в j-й группе.
