Падение плоской электромагнитной волны на диэлектрическое полупространство под произвольным углом

Рассмотрим случай, где плоская электромагнитная волна, падает на границу раздела под произвольным углом Ф, распространяясь в среде 1, удовлетворяющим условно 0<=Ф<=90.

На изображении показано направление осей координат и геометрия предоставленной задачи.

 

 

Из изображения следует, что вектор п_пад образует с положительными направлениями осей x, y и z углы 90,90-Ф и Ф соответственно. Поскольку cos90=0 и cos(90-ф)=sinф – комплексная амплитуда падающей волны, запись можно произвести следующим образом:

Если обозначить углы через ф` и Ψ, указанные на изображении выше и соответственно называемые углами преломления и отражения, то комплексные амплитуды преломленной и отраженной волн могут быть переданы в виде

в плоскости z=0, то есть на границе раздела, должны выполняться условия непрерывности тангенциальных составляющих векторов E и H, то есть

получим,

От того, что являются совершенно равноправными все точки поверхности раздела, соотношение должно являться тождеством относительно переменной у. Для этого нужно, чтобы всех экспонент показатели, входящих в выражение, были равны при всех у.

Предоставленное условие записано может быть в виде двух равенств:

ф=ф`

sinф/sinΨ=β₂/β₁

Тем самым, получены два закона хорошо известных из элементарной физики, определяющих поведение волн на границе раздела двух сред. Закон равенства углов падения и отражения – первый из них, второй носит название закона Сиелля.

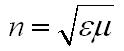Получим

sinф/sinΨ=n₂/n₁