Ток смещения— величина, прямо пропорциональная быстроте изменения электрической индукции.
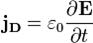Плотность тока смещения
Материальные уравнения эл/м поля
Для описания электромагнитных явлений в материальных средах необходимо располагать соотношениями, которые связывали бы попарно векторные поля Е и D, В и Н. Уравнения подобных связей принято называть материальными уравнениями.
Третье уравнение Максвелла является обобщением закона Гаусса на случай переменных процессов. Поток вектора электрической индукции D через поверхность S, ограниченную объемом V равен электрическому заряду сосредоточенному внутри объема V:
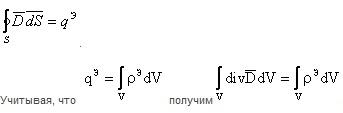
Последнее соотношение справедливо, если равны подынтегральные соотношения. Отсюда получаем: div D= ρ(свободных зарядов) (1)
Это уравнение обобщеная форма закона Гаусса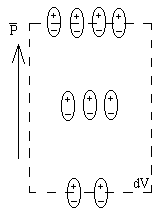 
. Развернем дивергенцию в системе координат:
 |
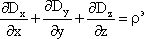Анализируя (1) отметим, что истоками или стоками вектора электрического смещения D являются свободные электрические заряды. Силовые линии начинаются на положительных зарядах и заканчиваются на отрицательных. В отличие от вектора электрического смещения истоками и стоками другого электрического вектора - вектора напряженности H могут быть как свободные, так и связанные электрические заряды.
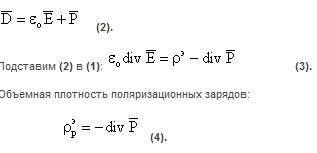
Причиной возникновения этой величины является неравномерность вещества под действием внешнего электрического поля. Подставляя (4) в (3), получим:
Так как в природе не обнаружено магнитных зарядов и токов, то закон Гаусса и его дифференциальная форма в этом случае описываются следующим образом:
Векторное поле магнитной индукции не имеет стоков и истоков. Силовые линии замкнуты.
D=ε0E
B=μ0H
Эти два уравнения называют материальными уравнениями.
