Хвилі типу Е - електричні хвилі

Умова: , .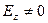

Запишемо рівняння Гельмгольца відносно E_z в циліндричній системі координат - вираз (50)

. (93)

Розв'язуючи це рівняння методом розділення змінних отримаємо

. (94)

Оскільки точка г=0 знаходиться зовні тої області, де є е. м. п. хвилі, то в вирішенні (62) нема потреби відкидати функцію Неймана N_m, яку не враховують в задачі для круглого хвилеводу. Використаємо граничну умову і отримаємо

. (95)

Ця система однорідних лінійних алгебраїчних рівнянь має нетривіальне вирішення (тобто , ) в тому випадку, коли визначник її дорівнює нулю, (det=0), тобто

. (96)

Знайшовши визначник по правилу Крамера, маємо

. (97)

Це співвідношення уявляє собою трансцендентне рівняння відносно по­перечного хвильового числа .

Якщо задати m та R₂/R₁, рівняння може бути вирішене чисельно, або графічно. При цому може бути знайдено n його коренів, тому хвиля позна­чається Е_mn.

Аналіз показує, що найнижчим типом хвиль серед хвиль типу Е для ко-аксіалу є хвиля Е₀₁.