Магнітні хвилі (Н) колового хвилеводу

Умова хвиль типу Н - , .

Вирішення хвилевого рівняння для H_z проведемо аналогічно хвилі типу Е і в результаті отримаємо результат:

(85)

Щоб знайти поперечні складові підставимо (85) в (11) та (12) з урахуванням вира-

зу для в циліндричній системі координат і отримаємо

(86)

В (86) штрих позначує похідну , тобто по всьому аргументу.

Для визначення використаємо граничну умову (41) для H_z - 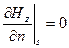; для колового хвилеводу напрямок нормалі протилежний по напрямку з ортом -

рис. 2.21.

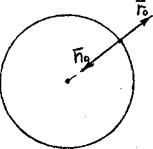
Рисунок 2.21 - Орти та для КХ

 

Як і для хвилі типу Е, одержимо

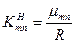, (87)

де - n-тий корень похідної від функції Беселя порядку m.

 

 

Як відомо , і підставивши сюди (87), отримаємо

. (88)

Як видно з Таблиці 1 найменше значення серед 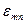та має корень , тому хвиля Н₁₁ є основною хвилею круглого хвилеводу.

Звернемо увагу також на те, що , , 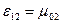і т.д. Це є проявою наступної властивості функцій Беселя та їх похідних

якщо , то , тобто , а звідси витікає, що .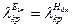

Таким чином, в коловому хвилеводі хвилі типу Е_1n та Н_0n будуть вирод­женими.

Розглянемо структуру поля основної хвилі Н₁₁ для КХ - рис. 2.22.

 

Рисунок 2.22 - Структура поля хвилі Н_п для КХ

 

Ця структура де в чому нагадує хвилю Н₁₀ в ПХ, але добавляється та .

Серед хвиль типу Н в КХ цікаву та корисну властивість має хвиля типу Н₀₁. Вона полягає в тому, що при збільшені частоти стала втрат зменшується. Це використовується для розробки хвилеводних ліній передачі, а також коли­вальних систем з унікально вузькою АЧХ. Розглянемо структуру поля хвилі H₀₁ – рис. 2.23. Поле цієї хвилі, як і хвилі Е₀₁, не залежить від азимутальної координати φ.

 

Рисунок 2.23 - Структура поля хвилі Н₀₁ для КХ (в перерізі В-В присутня лише складова H_z)

 

Дослідимо графічно залежність H_z(r) для хвилі Н₀₁ - рис. 2.24.

 

Рисунок 2.24 - до пояснення розподілу H_z(r) хвилі Н₀і для КХ

 

Тут розподіл H_z(r), як виходить з (85), диктує функція 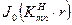, але не до значення (перший корень фуцнкції J₀), а до значення 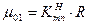(пер­ший корень функції 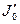, бо це хвиля типу H₀₁). По цій причині H_z(r) для хвилі Н₀₁ має два максимуми:

- при г=0, тобто у центрі хвилеводу ;

- при r=R, тобто на поверхні хвилеводу .

Враховуючи, що , можна зробити висновок, що

H_z(R)<H_z(0), причому зі збільшенням частоти цей ефект посилюється, тобто е.м.п. начебто "відтісняється" від поверхні хвилеводу. Таким чином, зі збільшенням частоти зменшується густина поверхневого струму на поверхні хвилеводу, що призводить до зменшення втрат.

Розглянемо діаграму хвиль круглого хвилеводу.