Линейный алгоритм – это алгоритм, в котором блоки выполняются последовательно сверху вниз от начала до конца. Основу линейного алгоритма составляют три алгоритмические конструкции.
Операция ввода позволяет задать значения исходных данных алгоритма, необходимых для выполнения дальнейших расчетов. По сути дела, эта операция означает, что в ячейку памяти, отведенную компьютером под некоторую переменную, нужно поместить константу. На реальном компьютере эта константа может быть введена самыми разными способами, например, введена с клавиатуры, получена из заранее подготовленного файла или от внешнего устройства, подключенного к компьютеру;
Операция присваивания используется для задания значения некоторой переменной, обычно она имеет вид переменная=значение или переменная:=значение, знак = или:= читается в этом случае как "присвоить". При присваивании сначала берется (или вычисляется) значение справа от знака "присвоить", затем это значение записывается в переменную. В большинстве языков программирования существуют схожие требования к именам (идентификаторам) переменных и других объектов данных, используемых программистом:
· имена могут включать латинские буквы, цифры и знак подчеркивания (в конкретном языке программирования возможны и другие символы, разрешенные в идентификаторах, опустим их для простоты);
· идентификатор состоит из одного слова; если требуется пробел в имени, он заменяется на подчеркивание: так, My_1 будет правильным именем объекта, а My 1 - нет;
· имя всегда начинается с буквы, например, возможен объект с именем A1, но не 1A; прописные и строчные буквы в именах могут как различаться, так и не различаться в конкретном языке;
· имена не могут совпадать с зарезервированными в языке служебными словами, обозначающими встроенные в этот язык операции над данными.
Кроме того, обычно переменные должны иметь определенный тип данных, назначенный программистом. Подробнее о типах данных говорится в п. 1.8.
Справа от знака "присвоить" может находиться не только переменная или константа, но и арифметическое выражение (формула). Арифметические выражения строятся из операндов, которыми могут быть константы, переменные и стандартные функции. В выражение также могут входить арифметические операции и круглые скобки. В большинстве языков определено 6 арифметических операций, перечислим их в соответствии с приоритетом, т. е., старшинством (табл. 2). Операции с одинаковым приоритетом равноправны между собой и выполняются слева направо, как и в математике.
Таблица 2. Арифметические операции
| Приоритет | Обозначение операции | Описание операции |
| * | Умножение | |
| / | Деление | |
| div | Деление 2 целых значений с отбрасыванием остатка | |
| mod | Взятие остатка от деления 2 целых значений | |
| + | Сложение | |
| - | Вычитание |
Операции div и mod определены только для целочисленных операндов. Приведем пример их использования:
y:=2012;
c:=y div 100;
n:=y mod 100;
Здесь переменная c получит значение 20, а n - значение 12.
Стандартные функции включены в любой развитый язык программирования и служат для выполнения элементарных математических расчетов, часто требуемых при написании программ. Наборы этих функций различны в разных языках, но все функции оформляются одинаково: после имени функции следует ее аргумент, заключенный в круглые скобки. Если аргументов несколько, они разделяются запятыми, например sin(x) означает вычисление синуса от значения переменной x, выполняемое стандартной функцией, а запись z:=max(x,y) может означать вызов стандартной функции определения максимального из двух значений. Результатом вызова функции будет то, что значение z будет установлено в большее из значений x и y.
При необходимости изменить обычное старшинство операций в записи выражения используются дополнительные круглые скобки. Например, правильная запись выражения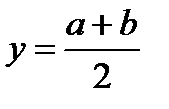 
выглядит как y:=(a+b)/2. Запись y:=a+b/2 неверна, т. к. это означает 
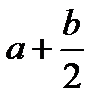. Разумеется, все скобки в выражении должны быть парными и располагаться справа от знака присваивания. Кроме того, в записи арифметических выражений нельзя пропускать знак умножения *, как часто делается в математике: выражение 4ac записывается как 4*a*c. Нельзя писать sin*x или sin x, после имени функции может следовать только ее аргумент в круглых скобках.
Третьей типовой конструкцией линейного алгоритма является операция вывода, позволяющая отобразить на экране (а также вывести на бумагу, записать во внешний файл и т.д.) значения переменных которые являются выходными данными алгоритма и которые к этому моменту сохранены в соответствующих ячейках памяти операторами присваивания.
На рис. 1 приведен пример блок-схемы алгоритма вычисления площади прямоугольника s по известным длинам сторон a, b.
Исходные данные: a- длина прямоугольника, b- ширина прямоугольника.
Выходные данные: s – площадь.
| Начало |
| Ввод a,b |
| Вычисление s=a*b |
| Вывод площади s |
| Конец |
Рис. 1. Блок – схема линейного алгоритма
Запись структуры алгоритма на псевдокоде выглядит следующим образом:
1. начало
2. ввод a,b
3. вычисление s=a*b
4. вывод s
5. конец
Разветвляющийся алгоритм позволяет организовать в программе проверку условий и реализуется по одному из нескольких направлений вычисления (ветвей алгоритма). Выбор одной из ветвей зависит от истинности или ложности некоторого условия (логического выражения), включенного в состав условного оператора. Программа должна учитывать все возможные ветви вычислений. При запуске программы, в зависимости от данных, выполняется только одна из возможных ветвей.
Неполный (короткий) условный оператор если–то, на блок-схеме изображается следующим образом (рис. 2):
| Условие |
| Да |
| Оператор1 |
Рис. 2. Блок-схема короткого условного оператора
Если условие истинно (выполняется), то выполняется и оператор1, иначе оператор1 игнорируется. В качестве этого оператора может быть указано любое разрешённое в алгоритмическом языке действие.
Полный условный оператор если–то–иначе на блок-схеме изображается следующим образом (рис. 3):
Оператор 1
Условие
Да
Нет
Оператор 2
Рис. 3. Блок-схема полного условного оператора
Если условие истинно, то выполняется оператор1, иначе выполняется оператор2. Всегда выполняется только один из двух операторов.
Более сложную конструкцию представляет собой составной условный оператор. Он применяется, когда есть более двух вариантов расчета. Общий вид составного оператора может включать произвольное число условий и ветвей расчета:
если условие1 то оператор1
иначе если условие2 то оператор2
...
иначе если условиеN то операторN
иначе оператор0;
При использовании оператора последовательно проверяются условия 1, 2,..., N, если какое-то из них выполняется, то выполняется соответствующий оператор с номером 1, 2,..., N и затем управление передается на оператор, следующий за условным. Если все условия ложны, выполняется оператор0 (если он задан). Число ветвей N не ограничено, ветви иначе оператор0; может и не быть.
Существенно то, что если выполняется более одного условия из N, обработано все равно будет только первое истинное условие.
Для случаев, когда требуется выбор одного значения из конечного набора вариантов, составной условный оператор удобнее заменять оператором выбора (переключателем). В большинстве языков он обозначается ключевым словом case или switch и выполняется так же, как составной условный оператор.
В качестве примера приведем блок-схему алгоритма, позволяющего вывести большее из двух заданных значений a,b (рис. 4).
Исходные данные: a- первое число, b- второе число.
Выходные данные: вывод наибольшего числа.
| a>b |
| Да |
| Нет |
| Начало |
| Ввод a,b |
| Вывод b |
| Вывод a |
| Конец |
Рис. 4. Алгоритм с полным условным оператором
Запись условного алгоритма на псевдокоде имеет следующий вид:
1. начало
2. ввод значений a и b
3. если а>b то вывод a,
4. иначе вывод b
5. конец
Задачу можно было решить и с использованием неполного условного оператора если–то. Такое решение изображено на рис. 5
Запись алгоритма с рис. 5 на псевдокоде выглядит следующим образом:
1. начало
2. ввод двух значений a и b
3. если а>b то вывод a
4. если b>=a то вывод b
5. конец
| Начало |
| Ввод a,b |
| a>b |
| Да |
| Нет |
| Вывод a |
| Конец |
| b>=a |
| Да |
| Нет |
| Вывод b |
Рис. 5. Блок-схема с неполными условными операторами
Когда после ключевых слов то или иначе вновь используются условные операторы, они называются вложенными. Число вложений может быть произвольно, при этом действует правило: ветвь иначе всегда относится к ближайшему сверху оператору если, для которого ветвь иначе еще не указана. Часто вложением условных операторов можно заменить использование составного.
В качестве примера рассмотрим алгоритм для определения номера координатной четверти p, в которой находится точка с координатами (x,y). Для простоты примем, что точка не лежит на осях координат. Без использования вложений основная часть алгоритма в записи на псевдокоде может иметь следующий вид:
если (x>0) и (y>0) то p:=1
иначе если (x<0) и (y>0) то p:=2
иначе если (x<0) и (y<0) то p:=3
иначе p:=4;
Операция "и" (and) в этом примере, требует одновременного выполнения двух условий, подробнее эта и другие логические операции рассмотрены в п. 1.8.
Использование такого количества условий представляется явно избыточным. Перепишем программу, используя тот факт, что каждое из условий x>0, x<0 оставляет в качестве значения p только по две возможных четверти из четырех:
если x>0 то
если y>0 то p:=1
иначе p:=4;
иначе
если y>0 то p:=2
иначе p:=3;
В первом фрагменте программе проверяется от двух до шести условий, во втором - всегда только два условия. Здесь использование вложений дало существенный выигрыш в производительности.
В большинстве языков программирования ключевое слово "если" записывается как if, "то" – then, "иначе" – else.
Циклический алгоритм (или циклический вычислительный процесс) характеризуется повторением одних и тех же вычислений над некоторым набором данных. Числом повторений цикла управляет специальная переменная, называемая его счетчиком или управляющей переменной цикла. На счетчик накладывается условие, определяющее, до каких пор следует выполнять цикл.
Повторяемый блок вычислений называют телом цикла. В теле цикла должно быть обеспечено изменение значения счетчика, чтобы он мог завершиться. Однократное выполнение тела цикла называют его шагом.
Таким образом, для программирования цикла достаточно определить условие, управляющее числом его повторений и описать операторы, образующие тело цикла. С этой точки зрения, теоретически возможны всего два вида циклов - проверка условия либо предшествует выполнению тела цикла, либо происходит после него. Изобразим эти циклы в виде блок-схем (рис. 6).
В цикле с предусловием сначала проверяется условие, затем, в зависимости от того, истинно оно или ложно, либо выполняется тело цикла, либо следует переход к оператору, следующему за телом цикла. После завершения тела цикла управление вновь передается на проверку условия. Естественно, предполагается, что в теле цикла было обеспечено некоторое изменение входящих в условие переменных - в противном случае произойдет зацикливание и программа "зависнет".
Цикл с предусловием можно описать следующим псевдокодом:
нцпока условие
тело цикла (операторы)
кц
В большинстве языков программирования цикл с предусловием записывается с помощью ключевых слов while … do., часто его называют просто "цикл while".
Для цикла с постусловием сначала выполняется тело цикла, затем управление передается на проверку условия. В зависимости от истинности или ложности условия, тело цикла выполняется повторно или же происходит переход к оператору, следующему за телом цикла. Все, сказанное о возможном зацикливании для цикла с предусловием, справедливо и для цикла с постусловием.
Цикл с постусловием описывается таким псевдокодом:
нц
тело цикла (операторы)
пока условие
кц
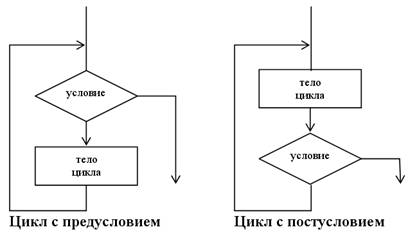
Рис. 6. Блок-схемы циклов с предусловием и постусловием
Исходя из приведенных блок-схем, очевидно основное различие двух циклов: цикл с постусловием гарантированно выполняется хотя бы раз, а цикл с предусловием может не выполняться ни разу, если условие сразу же окажется ложным. В то же время, оба рассмотренных вида циклов сходны тем, что число их повторений не задано в явном виде (хотя обычно может быть вычислено).
Цикл с постусловием записывается с помощью ключевых слов do … while (Си-подобные языки) или repeat … until (паскалеподобные).
Рассмотрим пример алгоритма с циклом, имеющим наперед неизвестное количество проходов. Для этого решим следующую задачу: указать наименьшее количество членов ряда натуральных чисел 1, 2, 3,..., сумма которых больше заданного значения К.
Блок-схема алгоритма решения этой задачи приведена на рис. 7. Задача может быть решена как с помощью цикла с предусловием, так и с помощью цикла с постусловием. В первом случае псевдокод имеет следующий вид:
1. начало
2. ввод K
3. s:=0, i:=1
4. нц пока s<=k
5. s:=s+i
6. i:=i+1
7. кц
8. вывод i, s
9. конец
| Да |
| Нет |
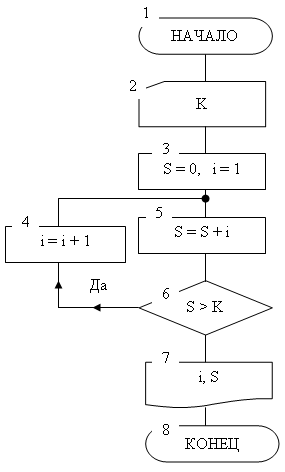
Рис. 7. Цикл с заранее неизвестным числом шагов
При использовании цикла с постусловием изменятся только строки с номерами 4-7:
4. нц
5. s:=s+i
6. i:=i+1
7. пока s<=k кц
В реальных задачах циклы с предусловием и постусловием также обычно взаимозаменяемы, хотя замена не всегда делается так же элементарно, как в приведённом примере.
Как в учебных, так и в реальных задачах циклы чаще всего обрабатывают не отдельные переменные, а массивы. Массивы нужны для хранения в памяти компьютера большого числа однотипных данных. В основе массивов лежит понятие индекса.
Допустим, нам известна температура в каждый из дней октября:
| День месяца | … | |||||||||||||||||
| Температура, °С | -2 | -4 | … |
Тогда температура - это последовательность чисел из нижней строки таблицы, а день месяца – это порядковый номер элемента в этой последовательности или индекс.
По таблице можно определить, что температура в первый день месяца была 5 градусов, во второй – 7, в десятый – 3, а в двадцать девятый - 0.
Если обозначить последовательность температур за весь месяц, например, буквой t, тогда можно обозначить через t(l) температуру первого дня месяца, t(2) - второго,..., t(31) -последнего. Теперь каждый из этих элементов последовательности обладает именем и значением, т. е. является переменной с индексом.
Таким образом, под массивом можно понимать набор однотипных данных, объединенных одним именем и отличающихся индексами.
В нашем примере имя массива t, а индекс может принимать любые целочисленные значения от 1 до 31. Обращение к элементу массива производится по имени массива и индексу, например, t(7) или t[7], при этом каждый элемент массива имеет свое значение. Если индекс массива имеет переменное значение i, то обращение к элементу массива можно осуществить как t(i).
Этот пример является определением одномерного массива, фактически, являющегося некоторым списком, а если данные можно представить в виде двумерной таблицы, то и массив можно определить как двумерный. Пример двумерного массива показан на рис. 8.
Элемент такого массива характеризуется двумя индексами: первый показывает строку, в которой расположена ячейка, второй – ее столбец. Например, запись d[2,5]=43 означает, что в ячейку, размещенную на пересечении 2-й строки и 5-го столбца двумерного массива d, нужно записать константу 43.
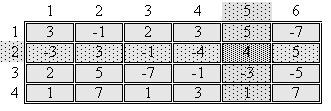
Рис. 8. Двумерный массив
Аналогично устроена структура трехмерных массивов и массивов большей размерности.
Массивы могут быть различных типов: числовые, строковые и т. д. Как правило, перед использованием массив нужно описать с помощью специального оператора, чтобы компьютер мог выделить под него оперативную память.
Теперь приведем пример алгоритма, содержащего цикл с наперед известным количеством шагов (повторений). Алгоритм решает задачу накопления суммы положительных элементов одномерного массива Z длины N (под длиной одномерного массива понимается количество его элементов). Блок-схема алгоритма показана на рис. 9. Приведем также решение на псевдокоде:
1. начало
2. ввод массива Z из N элементов
3. s=0, i=1
4. нц пока i<=N
5. если Z[i]>0 то s=s+Z[i]
6. i=i+1
7. кц
8. вывод s
9. конец
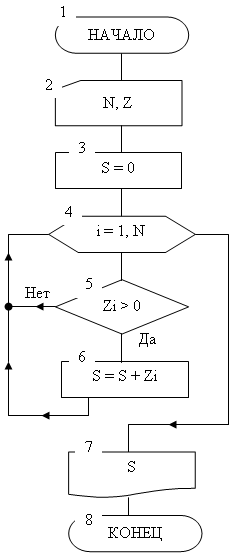
Рис. 9. Блок-схема цикла с заранее известным числом шагов
Заметим, что на практике для ввода массива Z из N элементов обычно требуется организовывать дополнительный цикл в программе. Как правило, ввод, вывод и обработка одномерных массивов осуществляются поэлементно с помощью рассмотренного далее цикла с параметром.
В случаях, когда объем последовательно обрабатываемых данных известен заранее (а значит, известно и требуемое число шагов цикла), а управляющая переменная меняется с шагом, равным единице, применяется такая форма цикла с предусловием, как цикл с параметром (распространены также названия цикл со счетчиком, цикл "для", обычно записывается ключевым словом for). В циклах с параметром число повторений полностью зависит от правила изменения управляющей переменной, которое задается с помощью начального и конечного значений параметра и, возможно, шага его изменения (в некоторых языках цикл реализован с произвольным шагом, не обязательно равным 1).
Приведем пример. Пусть i – параметр цикла, изменяющийся от 1 до 10 включительно с шагом изменения, равным 1. На каждом шаге цикла печатается слово "Привет". Такой цикл может быть изображен следующей блок-схемой (рис. 10):
| i=1, 10, 1 |
| Вывод слова "Привет" |
Рис. 10. Цикл с параметром
Алгоритм на псевдокоде:
1. начало
2. нц для i=1, 10, 1
3. вывод слова "Привет"
4. кц (Конец цикла)
5. конец
В ряде языков программирования, например, в С++, цикл for является, фактически, другой формой записи цикла while.
Нередко при алгоритмическом решении задачи возникает необходимость создания цикла, содержащего в своем теле другой цикл. Такие циклы называются вложенными или кратными. Порядок вложенности циклов, когда в теле внутреннего цикла содержатся другие циклы, может быть достаточно большим. Этот порядок определяется методом, с помощью которого достигается решение поставленной задачи. Так, при обработке двумерных массивов, как правило, требуется двойной цикл, чтобы последовательно перебрать строки и столбцы матрицы. При этом цикл, который содержит вложенный цикл, называется внешним, вложенный цикл называется внутренним. Управляющая переменная внутреннего цикла всегда меняется быстрее, чем переменная внешнего. Это означает, что для каждого значения переменной внешнего цикла перебираются все значения переменной внутреннего. В случае вложения нескольких циклов это правило также действует: быстрее всего меняется переменная самого внутреннего цикла.
