Вычисление площадей графическим способом состоит в том, что участки, изображенные на плане, разбивают на простейшие геометрические фигуры – преимущественно на треугольники, реже трапеции и прямоугольники. В каждой фигуре на плане измеряют высоту и основание, по которым вычисляется площадь. Сумма площадей фигур дает площадь участка.
Чем меньше углов имеет граница участка, тем меньше эффективность этого способа, следовательно, для вычисления площадей участков, имеющих большое количество углов, целесообразнее вычислять площадь по графическим координатам точек, т.е. по координатам, измеренным на плане при помощи измерителя или координатографа, координатометра и др., пользуясь формулами (3.6), (3.7).
Наилучшим вариантом разбивки участка на треугольники будет тот, при котором треугольники близки к равносторонним (вернее, высоты по величине близки основаниям).
При разбивке участка на простейшие фигуры можно принять много вариантов, однако, точность вычисления площади участка при различных вариантах не будет одинаковой. Погрешность вычисления площади каждого треугольника по высоте и основанию можно рассчитать по формуле (3.8).
Эта формула справедлива также для прямоугольника, параллелограмма и трапеции, площади которых вычисляют по двум величинам, измеренным по плану.
Погрешности измерения линий по плану можно считать одинаковыми, независимо от длин линий, т.е. mа = mh = m.
Тогда по формуле (3.8)
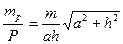. (3.9)
Так для треугольника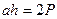 
, а для остальных фигур 
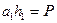, то согласно (3.9), для треугольника
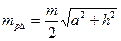, (3.10)
а для прямоугольника, параллелограмма и трапеции
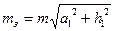, (3.11)
Если a=h, то для ∆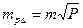 
. (3.12)
Для прямоугольника и параллелограмма (при a1=h1), а также трапеции при равенстве средней линии и высоты
.
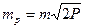Таким образом, площадь треугольника графическим способом вычисляется точнее, чем площади других фигур, следовательно, площадь при разбивке на треугольники вычисляется точнее, чем при разбивке на прямоугольники, трапеции и др.
Учитывая, что при разбивке фигуры на треугольники не всегда можно получить треугольники с одинаковыми основаниями и высотами погрешность площади участка можно вычислить по формуле
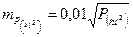
или для планов разных масштабов
,
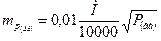где М- знаменатель численного масштаба плана.
