Для измерения площадей участков по результатам измерения линий и углов на местности применяют формулы геометрии, тригонометрии и аналитической геометрии. Рассмотрим наиболее употребительные из них.
Для учета площадей занятых строениями, усадьбами, площадей вспашки, посева, участки разбивают на простейшие геометрические фигуры, преимущественно треугольники, прямоугольники, реже трапеции. Площади участков определяют как суммы площадей отдельных фигур, вычисляемых по линейным элементам (высотам и основаниям) по общеизвестным формулам геометрии. При учете вспашки, посева, уборки урожая площади определяют также по длине маршрута агрегата и ширине его захвата.
Если по границам участка проложен теодолитный ход, то площадь всего участка или его части можно вычислить по следующим формулам:
Треугольник (рис.3.1, а). Определим его площадь по двум сторонам S1 и S 2 и углу β2, заключенному между ними.
Из рисунка видим, что
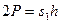(3.1)
но 
.
Подставив значение h в (3.1) получим
(3.2)
Рисунок 3.1 – Схемы определения площадей геометрических фигур
Четырехугольник. Зная четыре стороны S1, S 2, S3, S 4 и два противоположных угла β2 и β4 (рис.3.1,б), на основании формулы (3.2) получим
(3.3)
Если в четырехугольнике известны три стороны S1, S 2, S3 и два угла β2 и β3, заключенные между этими сторонами (рис.3.1, в), то площадь можно вычислить по формуле
. (3.4)
Пятиугольник (3.1, г). По пяти сторонам и трем углам β2, β4, β5 на основании формул (3.2) и (3.4) получим
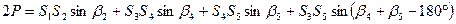. (3.5)
Такого же вида формулы можно получить для любого n - угольника, только с увеличением числа вершин n прогрессивно увеличивается количество слагаемых в формуле, поэтому при n >6 целесообразно вычислять площади по координатам вершин полигона, пользуясь формулами:
, 
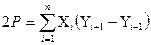(3.6)
и
. (3.7)
Чтобы площадь получилась положительной, номера точек полигона записывают в столбец ведомости всегда по ходу часовой стрелки. Число произведений в сумме равно числу точек.
Если площадь фигуры вычисляется по результатам измерений на местности, то точность вычисления площади можно рассчитать пользуясь теорией погрешности некоррелированных измерений
. (3.8)
Такую же формулу получим и для определения точности вычисления площади прямоугольника, параллелограмма и трапеции, у которой измеряется высота и средняя линия.
Если приближенно считать, что измерение линий на местности производится с относительной погрешностью
, то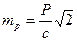 
, 
