Попробуем получить зависимость массы от скорости исходя из принципа относительности и закона сохранения импульса и энергии. Для этого возьмем простой случай упругого столкновения двух равных по массе частиц, движущихся навстречу друг другу с одинаковыми скоростями. Предположим, что импульс движущейся частицы - это вектор, всегда направленный по ее движению. Но мы не будем считать импульс пропорциональным скорости, как это делал Ньютон. Для нас он будет просто некоторой функцией скорости. Мы будем писать вектор импульса в виде вектора скорости, умноженного на некоторый коэффициент р = mv v. Индекс v у коэффициента будет напоминать нам, что это функция скорости v. Будем называть этот коэффициент «массой».
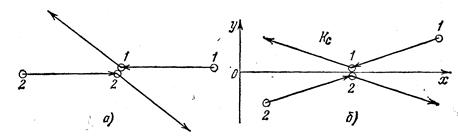
Картина столкновения частиц в системе центра масс представлена на рисунке (а). Общий импульс частиц до столкновения равен нулю. После столкновения их направления движения должны все равно остаться противоположными, потому что если это не так, то их суммарный вектор импульса будет отличен от нуля, т.е. не сохранится. Раз частицы одинаковы, то и скорости их должны быть одинаковы; более того, они просто должны остаться прежними, иначе энергия при столкновении изменится. Для удобства мы повернем оси, чтобы горизонталь делила пополам угол между направлениями частиц до и после столкновения (б).
Теперь взглянем на это столкновение с позиций наблюдателя, движущегося в автомашине со скоростью, совпадающей с горизонтальной компонентой скорости одной из частиц (система отсчета К /). Наблюдателю покажется, что частица 2 поднимается прямо вверх параллельно оси у (горизонтальная компонента у нее пропала), а после столкновения падает прямо вниз по той же причине (а). Зато частица 1 движется совсем иначе, она проносится мимо с колоссальной скоростью и под малым углом (но этот угол и до и после столкновения одинаков). Обозначим горизонтальную компоненту скорости частицы 1 через u, а вертикальную скорость частицы 2 - через w.
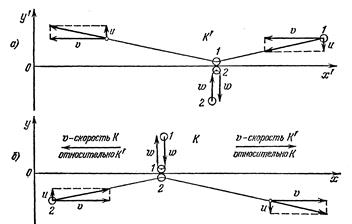
Наконец перейдем к системе отсчета К (б), относительно которой частица 1 движется параллельно оси у. Значения v, u, w в системе К и К / очевидно одинаковы вследствие симметрии задачи.
Для системы К потребуем сохранение импульса в у -направлении:
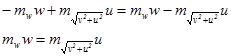
В системе К / игрековая компонента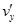 
начальной скорости частицы 2 равна w, а иксовая компонента 
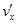= 0. В системе К игрековая компонента vy начальной скорости частицы 2 равна u. Относительная скорость систем К и К / равна v. Отсюда для определения связи между скоростями можно использовать формулу для преобразования поперечной скорости: 
. В нашем случае: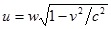 
. Поэтому закон сохранения импульса можно переписать:
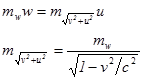
В последнем уравнении совершаем предельный переход w ®0 (практически w << c). При этом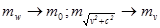 
. Таким образом, получаем нужную формулу:
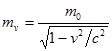
Рассмотрим интересное следствие. Для этого проанализируем неупругое столкновение двух одинаковых тел, сталкивающихся с одинаковыми скоростями w. При этом образуется новое тело, которое больше не распадается (рисунок). Предположив сохраняемость импульса и приняв принцип относительности, можно продемонстрировать интересное свойство массы вновь образованного тела.
Представим себе бесконечно малую скорость u, поперечную к скоростям w (можно было бы работать и с конечной скоростью u, но с бесконечно малыми значением u - проще), и посмотрим на это столкновение, двигаясь в лифте со скоростью u. Перед нами окажется картина, изображенная на рисунке (б). Составное тело обладает неизвестной массой М. У тела 1, как и у тела 2, есть компонента скорости u, направленная вверх, и горизонтальная компонента, практически равная w. После столкновения остается масса М, движущаяся вверх со скоростью u, много меньшей и скорости света, и скорости w. Импульс должен остаться прежним; посмотрим поэтому, каким он был до столкновения и каким стал потом. До столкновения он был равен р» 2 mwu, а потом стал р / = Мuu. Но Мu из-за малости u, по существу, совпадает с М 0. Благодаря сохранению импульса
М 0 = 2 mw.
Итак, масса покоя тела, образуемого при столкновении двух одинаковых тел, равна их удвоенной релятивисткой массе. Не правда ли странно? Тела вносят в суммарную массу не массу покоя, а больше. Оказывается, сохранение импульса в столкновении двух тел требует, чтобы образуемая ими масса была больше их масс покоя, хотя после столкновения эти тела сами придут в состояние покоя.
