с произвольными коэффициентами.
Рассмотрим уравнение вида 
С учетом обозначения 
можно записать:
При этом будем полагать, что коэффициенты и правая часть этого уравнения непрерывны на некотором интервале (конечном или бесконечном).
Теорема. Общее решение линейного неоднородного дифференциального уравнения 
в некоторой области есть сумма любого его решения и общего решения соответствующего линейного однородного дифференциального уравнения.
Доказательство. Пусть Y – некоторое решение неоднородного уравнения.
Тогда при подстановке этого решения в исходное уравнение получаем тождество:
Пусть 
- фундаментальная система решений линейного однородного уравнения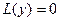 
. Тогда общее решение однородного уравнения можно записать в виде:
Далее покажем, что сумма 
является общим решением неоднородного уравнения.
Вообще говоря, решение Y может быть получено из общего решения, т.к. является частным решением.
Таким образом, в соответствии с доказанной теоремой, для решения линейного неоднородного дифференциального уравнения необходимо найти общее решение соответствующего однородного уравнения и каким- то образом отыскать одно частное решение неоднородного уравнения. Обычно оно находится подбором.
На практике удобно применять метод вариации произвольных постоянных.
Для этого сначала находят общее решение соответствующего однородного уравнения в виде:
Затем, полагая коэффициенты Ci функциями от х, ищется решение неоднородного уравнения:
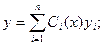
Можно доказать, что для нахождения функций Ci(x) надо решить систему уравнений:
