Решение различных геометрических, физических и инженерных задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту ил иную задачу, с какой – либо функцией этих переменных и производными этой функции различных порядков.
В качестве примера можно рассмотреть простейший случай равноускоренного движения материальной точки.
Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле:
В свою очередь ускорение a является производной по времени t от скорости V, которая также является производной по времени t от перемещения S. Т.е.
Тогда получаем: 
- уравнение связывает функцию f(t) с независимой переменной t и производной второго порядка функции f(t).
Определение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.
Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.
Определение. Общим решением дифференциального уравнения называется такая дифференцируемая функция y = j(x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.
Свойства общего решения.
1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.
2) При каких- либо начальных условиях х = х0, у(х0) = у0 существует такое значение С = С0, при котором решением дифференциального уравнения является функция у = j(х, С0).
Определение. Решение вида у = j(х, С0) называется частным решением дифференциального уравнения.
Определение. Задачей Коши (Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = j(х, С0), удовлетворяющего начальным условиям у(х0) = у0.
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную 
, то какова бы не была точка (х0, у0) в области D, существует единственное решение 
уравнения , определенное в некотором интервале, содержащем точку х0, принимающее при х = х0 значение j(х0) = у0, т.е. существует единственное решение дифференциального уравнения.
Определение. Интегралом дифференциального уравнения называется любое уравнение, не содержащее производных, для которого данное дифференциальное уравнение является следствием. 
Дифференциальные уравнения первого порядка.
Определение. Дифференциальным уравнением первого порядка называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:
Если такое соотношение преобразовать к виду то это дифференциальное уравнение первого порядка будет называться уравнением, разрешенным относительно производной.
Преобразуем такое выражение далее:
Функцию f(x,y) представим в виде: 
тогда при подстановке в полученное выше уравнение имеем:
это так называемая дифференциальная форма уравнения первого порядка.
- Уравнения с разделяющимися переменными
Определение. Дифференциальное уравнение называется уравнением с разделяющимися переменными, если его можно записать в виде
- 
.
Такое уравнение можно представить также в виде:
- 
Перейдем к новым обозначениям 
Получаем: 
После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.
Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.
Линейные уравнения.
Определение. Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:
при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением.
P(x) и Q(x)- функции непрерывные на некотором промежутке a < x < b.
Линейные однородные дифференциальные уравнения.
Рассмотрим методы нахождения общего решения линейного однородного дифференциального уравнения первого порядка вида
.
Для этого типа дифференциальных уравнений разделение переменных не представляет сложностей.
Общее решение: 
Линейные неоднородные дифференциальные уравнения.
Для интегрирования линейных неоднородных уравнений (Q(x)¹0) применяются в основном два метода: метод Бернулли и метод Лагранжа.
Метод Лагранжа.
(Ларганж Жозеф Луи (1736-1813) - французский математик, през. Берлинской АН,
поч. чл. Пет. АН (1776)).
Метод Лагранжа решения неоднородных линейных дифференциальных уравнений еще называют методом вариации произвольной постоянной.
Вернемся к поставленной задаче:
Первый шаг данного метода состоит в отбрасывании правой части уравнения и замене ее нулем.
Далее находится решение получившегося однородного дифференциального уравнения:
.
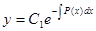Для того, чтобы найти соответствующее решение неоднородного дифференциального уравнения, будем считать постоянную С1 некоторой функцией от х.
Тогда по правилам дифференцирования произведения функций получаем:
