Пример 1. Решить относительно х:
| (1) |
а). Пусть а = 0, тогда –2х+4 = 0 Û х = 2;
б). Пусть а ¹ 0, тогда D = 1– 4а; при 1– 4а < 0 Þ а > 
х Î Æ;
при 1– 4а ³ 0 Þ а £ 
.
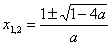Ответ: при а = 0 х = 2; при а ¹
0 и а £
уравнение (1) имеет два решения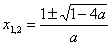
; при а ¹ 0 и а >
уравнение (1) не имеет решений.
При исследование квадратичной функции мы используем теоремы, которые также
помогают при решение задач с параметрами.
Т1. Если приведённое квадратное уравнение имеет два корня и b > 0,
c > 0, то оба корня этого уравнения отрицательные; b
< 0, c > 0, то оба корня этого уравнения
неотрицательны.
Т2. Необходимые и достаточные условия, чтобы корни квадратного
уравнения были больше заданного числа d:
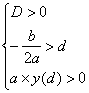
Пример 2. При каких значениях параметра а, корни уравнения неотрицательны:
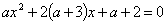
| (1) |
Разделим уравнение (1) на а, но поставим условие а ¹ 0, тогда получим
 
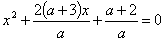
| (2) |
По Т1: 
;
1). D =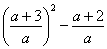 
; приводим к общему знаменателю а2, получаем
; 
.
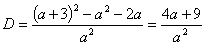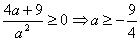2). 
> 0;
корень уравнения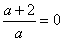 
:
а = –2 и а ¹ 0. Нанесем полученные точки на
координатную прямую (Рис. 1).
Получаем а < –2, а > 0
|
3). 
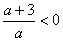; корень уравнения 
: а = –3
и а ¹ 0. Нанесем полученные точки на координатную прямую (Рис. 2).
Получаем –3 < а < 0.
|
4). Объединим полученные результаты:
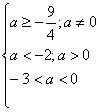
| (Рис. 3) |
Получаем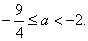 
|
Ответ: при 
уравнение (1) имеет неотрицательные корни.
Пример 3. При каких значениях параметра а, корни уравнения больше 1:
| (1) |
По Т2: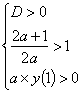 
.
1). 
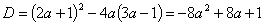
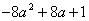> 0, разделим получившееся неравенство на –8, получаем
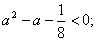корни данного
уравнения: 
.
Нанесем полученные точки на координатную прямую (Рис. 4).
|
Получаем 
< а < 
2). 
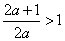, помножим обе части данного неравенства на 2 а, при этом а ¹ 0;
2а + 1 > 2а Þ 2а – 2а > –1 Þ 0 > –1 Þ а Î R.
3). Y(1) = 2а –2;
корни уравнения 2а(а-1) > 0: а1 = 0; а2 = 1.
Нанесем полученные точки на координатную прямую (Рис. 5).
|
Получаем а < 0, а > 1
4). Объединим полученные результаты:
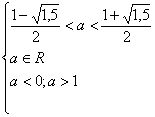
| (Рис.6) |
|
Получаем 
Ответ: при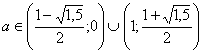 
корни уравнения (1) больше 1.
Пример 4. При каком наибольшем целом а оба корня уравнения заключены
строго между –2 и 4:
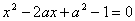Способ 1:
| (1) |
; тогда корни уравнения (1):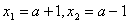 
. Они должны быть заключены строго между –2 и 4:
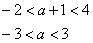
Нанесем полученные точки на координатную прямую (Рис. 7).
Получаем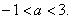 
|
Способ 2:
По Т2:
1). D = 1 > 0;
2). 
;
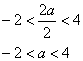3). Y(–2) = а2+4а+3
а2+4а+3 > 0; корни уравнения а2+4а+3 =
0: а1 = –3, а2 = –1; нанесем
полученные точки на координатную прямую (Рис. 8).
|
|
Получаем а < –3, а > –1.
Y(4) = а2–8а+15
а2–8а+15 > 0; корни уравнения а2–8а+15 =
0: а1 = 3, а2 = 5; нанесем полученные
точки на координатную прямую (Рис. 9).
|
Получаем а < 3, а > 5.
4). Объединим полученные результаты:
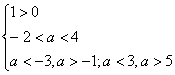
| (Рис.10) |
|
Получаем –1 < а < 3.
Ответ: при а = 2 оба корня уравнения (1) заключены строго между –2 и 4.
Пример 5. Найти коэффициент а, если корни уравнения связаны соотношением
2х1+х2 = 3:
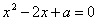
по теореме Виета: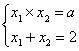 
;
составим и решим систему: 
получаем х1 = 1, х2 = 1, тогда
а = 1.
Ответ: а = 1.
http://www.coolreferat.com/Уравнения_с_параметрами
или здесь посмотрите
ссылка на презентацию, здесь можно взять с 1 по 8 слайд
http://nsportal.ru/ap/ap/nauchno-tekhnicheskoe-tvorchestvo/reshenie-kvadratnyh-uravneniy-s
