Пример 1. Решить относительно х:
 .
| (1) |
По смыслу задачи (m-1)(x+3) ¹ 0, то есть m ¹ 1, x ¹ –3.
Умножив обе части уравнения на (m-1)(x+3), получим уравнение
, получаем
.
Отсюда при m ¹ 2,25 
.
Теперь необходимо проверить, нет ли таких значений m, при которых
найденное значение x равно –3.
,
решая это уравнение, получаем, что х равен –3 при т = –0,4.
Ответ: при т ¹ 1, т ¹ 2,25,
т ¹ –0,4 уравнение (1) имеет единственное решение
; при т = 2,25 и при т = –0,4 решений нет, при т
= 1 уравнение (1) не имеет смысла.
Пример 2. Решить относительно х:
| (1) |
ОДЗ: х ³ – а, х ³ 0;
Поскольку уравнение (1)Û
Û 
| (2) |
и левая часть уравнения (2) неотрицательна, дополнительно к условиям
ОДЗ налагаем условие а ³ 0;
Þ
 ;
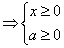| (3) |
при этих условиях
;
теперь к условиям (3) добавляем ещё условие
 ;
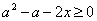в условиях (3), (4) имеем
| (4) |
при а = 0 х = 0 в силу условий (3), (4); при
а > 0 х 
; отсюда, добиваясь выполнения условия (4), получаем
Ответ: при а = 0 х = 0; при а ³
1 уравнение (1) имеет единственное решение х
; при а < 0, 0 < а < 1
уравнение (1) не имеет решений.
Пример 3. Решить относительно х:
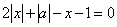
| (1) |
а). Х ³ 0,
;
по условию х ³ 0, то есть параметр должен удовлетворять условию
б). Х < 0,
по условию х < 0, то есть
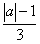< 0 
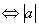< 1;
.
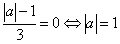Ответ: при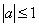 
уравнение (1) имеет два решения 
при 
> 1
уравнение (1) не имеет решений.
