Ученики должны понять, что решение уравнения с параметрами при заданных конкретных условиях – это частные решения уравнений. Например, задание может звучать так: «При каких значениях параметра … уравнение …. Имеет единственное решение или не имеет корней, или имеет корень равный… и т.д.
Пример1. При каких целых значениях параметра а уравнение  имеет целые корни.
имеет целые корни.
Решение: Приведём уравнение к виду  , если
, если  то
то  . Чтобы х был целым числом, необходимо, чтобы значение выражения
. Чтобы х был целым числом, необходимо, чтобы значение выражения  было делителем числа 5, то есть
было делителем числа 5, то есть  может быть равно 1; -1; 5; -5. Отсюда, а = 3; 1; 7;-3.
может быть равно 1; -1; 5; -5. Отсюда, а = 3; 1; 7;-3.
Ответ: при а = -3; 1; 3; 7.
Пример 2. При каких значениях параметра n уравнение 
а) имеет единственный корень;
б) имеет бесконечное множество корней;
в) не имеет корней.
Решение: 1. Выражения  имеют смысл при любых значениях n/
имеют смысл при любых значениях n/
2. Если  , то
, то 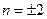 . При
. При  значение выражения
значение выражения 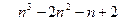 равно 0. Получаем уравнение вида
равно 0. Получаем уравнение вида  . Оно имеет бесконечное множество корней, то есть х – любое число. При
. Оно имеет бесконечное множество корней, то есть х – любое число. При  значение выражения
значение выражения 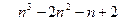 равно – 12, получается уравнение
равно – 12, получается уравнение  , которое не имеет корней.
, которое не имеет корней.
3. При  и
и  уравнение имеет единственный корень.
уравнение имеет единственный корень.
Ответ: а) При  и
и  .
.
б) При  . в) При
. в) При  .
.
Пример 3. При каком значении параметра а уравнение не имеет корней  .
.
Перепишем данное уравнение в виде  Если а = 2, то уравнение не имеет корней. Ответ: а = 2
Если а = 2, то уравнение не имеет корней. Ответ: а = 2
Пример 4. Найдите все значения параметра а, при каждом из которых число 7 является единственным корнем уравнения.
Решение: Способ I: Если для некоторого значения параметра число 7 является корнем уравнения, то для этого значения а справедливо равенство  , или равенство
, или равенство  .
.
Равенство справедливо при а = 0 или при а =1.
Внимание! Мы ещё не получили ответа, так как нашли два значения параметра а, предполагая, что число 7 является корнем уравнения. Но этот корень должен быть единственным, поэтому ещё требуется проверить, является ли число 7 единственным корнем уравнения
при а = 0 или при а =1.
Если а = 0, то уравнение перепишем в виде х – 7 = 0.
При а = 0 число7 является единственным корнем уравнения.
Если же а =1, то уравнение перепишем в виде х - 7 = х – 7.
При а=1 любое действительное число является корнем данного уравнения. Следовательно, число 7 не является единственным корнем уравнения.
Способ II. Перепишем исходное уравнение в виде 
При а =1 корнем уравнения является любое число, то есть число 7 не является единственным корнем уравнения. Поэтому в уравнении а ≠1.
Но тогда это уравнение имеет единственный корень 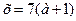 . Условие задачи будет выполнено, если это единственный корень есть число 7:
. Условие задачи будет выполнено, если это единственный корень есть число 7: 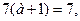 то есть при а = 0.
то есть при а = 0.
Ответ: а = 0.
Пример 5. Найдите все значения параметра а, при каждом из которых уравнения  и
и 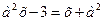 имеют общий корень.
имеют общий корень.
Решение: Перепишем первое уравнение в виде  . Это уравнение имеет корень лишь при
. Это уравнение имеет корень лишь при 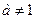 . Этот корень есть число
. Этот корень есть число 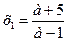 .
.
Перепишем второе уравнение в виде 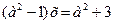 . Данное уравнение имеет корень лишь при
. Данное уравнение имеет корень лишь при  ,. Этот корень есть число
,. Этот корень есть число 
Осталось найти все значения параметра  . При каждом из которых первое и второе уравнение имеют общий корень, то есть х1 и х2 есть одно и то же число.
. При каждом из которых первое и второе уравнение имеют общий корень, то есть х1 и х2 есть одно и то же число.
Для этого решим уравнение 
Перенесём все слагаемые в одну часть уравнения и упростим разность алгебраических дробей, равносильное уравнение  которое имеет единственный корень
которое имеет единственный корень  . При этом значении а условие задачи выполнено.
. При этом значении а условие задачи выполнено.
Ответ: при 
Заключение.
Для реализации проекта мною были проанализированы методическая литература и учебные пособия, которые позволили выявить основные методы решения линейных уравнений с параметрами и адаптировать их к школьному курсу. Что помогло составить систему дидактических материалов, которые можно использовать для учащихся 8 классов в процессе усвоения той или иной темы или для параллельного повторения при подготовке к ГИА или ЕГЭ.
Литература
1. Амелькин В. В., Рабцевич В. Л. Задачи с параметрами: Пособие по математике. 3-е изд., доработ. - Минск: Асар, 2004.
2. Смыкалова Е.В. Математика. Модули, параметры, многочлены. Предпрофильная подготовка.-Сант-Петербург: СМИО Пресс,2006
3. В. В. Локоть. Задачи с параметрами. Учебное пособие.-Москва:Аркти,2003.




