Розв'язання

1. y - y_о = f '(x_o)(x – x_o) — рівняння шуканої дотичної.

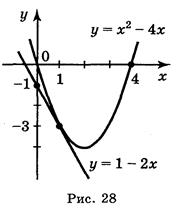
2. у_o= 1 ² – 4·1 = 1 – 4 = - 3.

3. .

4. Підставляємо значення x_o = 1, y_o = –3, f'(x_o) = –2 у рівняння дотичної: y + 3 = –2(x – 1), або у = – 3 – 2 x + 2, або y = –1 – 2 х (рис. 28).

 

 

Таблиця 4 Таблиця похідних

(е^x)’ = е^x

Похідна складеної функції у == f(g(x)) знаходиться за формулою

де u = g(x),

або похідна складеної функції дорівнює похідній зовнішній функції по проміжній змінній, помноженій на похідну внутрішньої функції по основному аргу­менту.

 

функція y = f(x) називається зростаючою на деякому проміжку, якщо для будь-яких х₁ і х₂, що належать проміжку, із умови х₂ > х₁ випливає, що f(x₂) > f(x₁).

Дотична в кожній точці графіка зростаючої функції, як видно з рис. 32, утворює з додатним напрямом осі ОХ або гострий кут, або кут, що дорівнює нулю (в останньому випадку дотична паралельна осі ОХ).

Виходячи із геометричного змісту похідної: tg α = f’(x_o), це означає, що похідна в кожній точці проміжку невід’ємна, тому для зростаючої функції f(x) виконується умова: .

Функція y = f(x) називається спадною на проміжку, якщо для будь-яких х₁ і х₂, що належать цьому проміжку, із умови х₂ > х₁ випливає, що f(x₂) < f(x₁). Дотична в кожній точці графіка спадної функції (рис. 33) утворює з віссю ОХ або тупий кут, або кут, що дорів­нює нулю, тому для функції f(x), яка спадає на деякому проміжку, вико­нується умова f'(x) < О.

На рис. 34 видно також, що одна і та ж функція може на одному про­міжку області її визначення зростати, а на іншому — спадати. Характер по­ведінки функції на кожному із цих проміжків визначається знаком її по­хідної.

Отже, наочне уявлення дозволяє сформулювати властивості зроста­ючих та спадних функцій.

Якщо функція у = f(x) диферен­ційована і зростає на деякому про­міжку, то її похідна на цьому про­міжку не від'ємна.

Якщо функція у = f(x) диференційована і спадає на деякому проміжку, то її похідна на цьому проміжку не додатна.

Проте для розв'язування задач особливо важливими є обернені твердження, які ви­ражають ознаки зростання і спадання функ­ції на проміжку. Нехай значення похідної функції у = f(x) додатні на деякому про­міжку, тобто f'(x) > 0. Оскільки f'(x) = tg α, то із умови tg α > 0 випливає, що дотичні, проведені до графіка функції в будь-якій точці цього інтервалу, утворюють гострі кути з додатним напря­мом осі ОХ. У цьому випадку графік функції «піднімається» на заданому проміжку, тобто функція зростає (рис. 35).

Якщо f'(x) < 0 на деякому проміжку, то кутовий коефіцієнт дотичної tg α = f(x) до графіка функції у = f(x) від'ємний. Це означає, що дотична до графіка функції утворює з віссю ОХ ту­пий кут і графік функції на цьому проміжку «опускається», тоб­то функція f(x) спадає (рис. 36).

Якщо f'(x) > 0 на проміжку, то функція f(x) зростає на цьому проміжку.

Якщо f(x) < 0 на проміжку, то функція f(x) спадає на цьому проміжку.

Ці два твердження називаються ознака­ми зростання (спадання) функції на про­міжку.

Строге доведення цих тверджень виходить за рамки шкільного курсу математики.

Проміжки зростання і спадання функції часто називають про­міжками монотонності цієї функції.

Знаходження проміжків зростання та спадання функції можна виконувати за таким планом:

1. Знайти область визначення заданої функції у = f(x).