Схема исследования:
1. Найти область определения функции (ООФ – значения переменной х, при которых функция существует).
2. Исследовать функцию на четность – нечетность:
Если f(-x)=f(x), то функция четная (график симметричен относительно оси О y).
Если f(-x)=-f(x), то функция нечетная (график симметричен относительно начала координат).
3. Найти вертикальные асимптоты.
!!! Вертикальные асимптоты х=х0 следует искать в точках разрыва функции y=f(x) или на концах ее области определения (a,b), если a и b - конечные числа.
Пусть функция y=f(x) определена в некоторой окрестности точки х0 (исключая, возможно, саму эту точку) и хотя бы один из пределов функции при х®х0-0 (слева) или х®х0+0 (справа) – равен бесконечности, т.е. lim f(x)=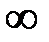 
или lim f(x)= 
. Тогда прямая х=х0 является вертикальной
х®х0-0 х®х0+0
асимптотой графика функции y=f(x).
4.Найти горизонтальные асимптоты (исследовать поведение функции в бесконечности).
Пусть функция y=f(x) определена при достаточно больших х и существует конечный предел функции lim f(x)=b. Тогда прямая y=b есть
x 
горизонтальная асимптота графика функции y=f(x).
Замечание. Если конечен только один из пределов lim f(x)=bл или
x 
lim f(x)=bп, то функция имеет левостороннюю y=b л или правостороннюю
x 
y=bп горизонтальную асимптоту.
5. Найти наклонную асимптоту.
Пусть функция y=f(x) определена при достаточно больших х и существуют конечные пределы функции lim 
и lim[f(x)-kx]=b.
x x
Тогда прямая y=kx+b является наклонной асимптотой графика функции y=f(x).
!!! Наклонная асимптота, так же, как и горизонтальная, может быть правосторонней или левосторонней.
6.Найти экстремумы (максимум, минимум) и интервалы монотонности (возрастание, убывание) функции.
- найти производную функции (разложить ее на множители) и приравнять ее к 0, т.е. 
;
- найти корни этого уравнения и точки, в которых производная не существует (критические точки);
- исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции (найти ординаты точек экстремума!);
- на промежутке, где 
- функция возрастает; на промежутке, где 
- функция убывает.
7.Найти точки перегиба и промежутки выпуклости и вогнутости функции
- найти вторую производную функции (разложить ее на множители) и приравнять ее к 0, т.е. 
;
- найти корни этого уравнения;
- исследовать знак второй производной слева и справа от каждой точки и сделать вывод о наличии точек перегиба функции (найти ординаты точек перегиба!);
- на промежутке, где 
- функция будет вогнутой; на промежутке, где 
- функция будет являться выпуклой вверх.
8.Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.
!!! Уравнение оси Ох: y=0.
Уравнение оси Oy: х=0.
9. Используя результаты исследования, построить график функции.
Необходимые формулы для решения задач о касательной
1. Общее уравнение прямой:
Ax+By+C=0
2. Уравнение прямой с угловым коэффициентом:
y=kx+b
(k=tgj коэффициент прямой равен тангенсу угла наклона этой прямой)
Если две прямые y=k1x+b1 и y=k2+b2 параллельны, то k1=k2.
Если две прямые y=k1x+b1 и y=k2+b2 перпендикулярны, то k1*k2=-1.
3. Уравнение прямой, проходящей через данную точку в данном направлении(известен коэффициент k):
Пусть прямая проходит через точку M1(x1;y1) и образует с осью Ox угол 
y-y1=k(x-x1)
4. Уравнение прямой, проходящей через две данные точки M1(x1;y1) и M2(x2;y2):
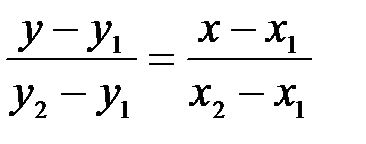
5. Уравнение касательной к кривой y=f(x) в точке x0 имеет вид
y-f(x0)=f¢(x0)(x-x0)
6. Геометрический смысл производной:
f¢(x0)=k=tga
(производная f¢(x0) есть угловой коэффициент(тангенс угла наклона) касательной, проведенной к кривой y=f(x) в точке x0)
