Определение. Функция 
называется возрастающей на множестве 
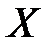, если для любых значени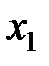й 
и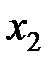 
из области определения: 
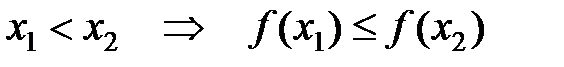, и убывающей, если для любых значени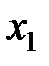й и 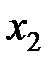из области определения: 
.
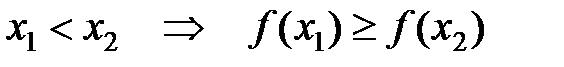Теорема (достаточное условие монотонности функции на отрезке). Пусть функция непрерывна на отрезке 
и дифференцируема на интервале 
. Тогда, если для любой точки 
интервала 
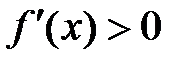, то функция 
– возрастающая на интервале и если 
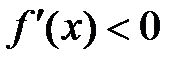, то – убывающая на интервале функция.
Геометрический смысл Если в некотором промежутке касательная к графику функции y=f(x) образует с осью Ox острый угол α (tg α˃0), то функция строго возрастает в этом промежутке. Если касательная к графику функции y=f(x) образует с осью Ox тупой угол α (tg α˂0), то функция строго убывает в этом промежутке (Рис. 4).
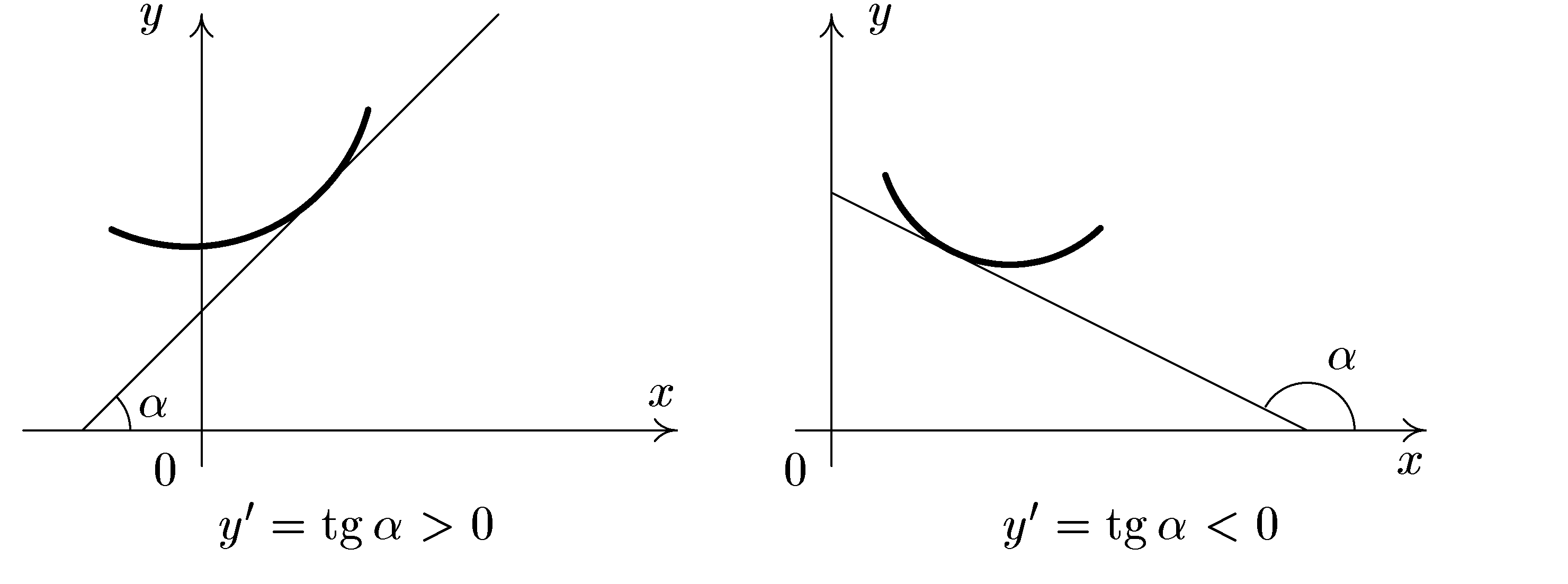
Рис. 4
