Определение. Точка 
называется точкой максимума функции 
, если существует такая 
-окрестность точки , что для всех 
из этой окрестности выполняется неравенство 
.
Определение. Точка называется точкой минимума функции , если существует такая -окрестность точки , что для всех из этой окрестности выполняется неравенство 
.
Определение. Экстремумом функции 
называется точка максимума или минимума функции.
Теорема (необходимое условие существования экстремума функции в точке). Пусть функция 
имеет в точке 
экстремум. Тогда производная 
либо равна нулю в точке 
, либо не существует.
Определение. Точки в которых производная равна 0 или не существует называются критическими.
!!! Критическая точка вовсе не обязательно является точкой экстремума.
Теорема (первое достаточное условие существования экстремума). Пусть функция – дифференцируемая функция.
1) Если в точке первая производная 
меняет свой знак с “+” на “–”, то функция имеет в точке максимум.
2) Если в точке первая производная меняет свой знак с “–” на “+”, то функция имеет в точке минимум.
Теорема (второе достаточное условие существования экстремума). Пусть функция дважды дифференцируема, причем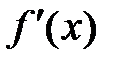 
и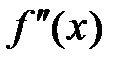 
– непрерывные функции. Тогда:
1) если 
и 
– точка минимума функции 
.
2) если и 
– точка максимума функции 
;
Рис.5
