Зако́н Ампе́ра — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила 
, с которой магнитное поле действует на элемент объёма 
проводника с током плотности 
, находящегося в магнитном поле с индукцией 
:
.
Если ток течёт по тонкому проводнику, то 
, где 
— «элемент длины» проводника — вектор, по модулю равный 
и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:
Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока 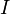 в проводнике и векторному произведению элемента длины проводника на магнитную индукцию :
 .
|
Направление силы определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила правой руки.
Модуль силы Ампера можно найти по формуле:
,
где 
— угол между векторами магнитной индукции и тока.
Сила 
максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции (
):
.
