Пусть постоянный ток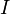 
течёт по контуру (проводнику) 
, находящемуся в вакууме, 
— точка, в которой ищется (наблюдается) поле, тогда индукция магнитного поля в этой точке выражается интегралом (в системе СИ)
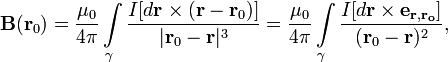
где квадратными скобками обозначено векторное произведение, r - положение точек контура , d r - вектор элемента контура, вдоль которого идет проводник (ток течет вдоль него);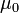 
- константа (магнитная проницаемость вакуума); 
- единичный вектор, направленный от источника к точке наблюдения.
§ В принципе контур может иметь ветвления, представляя собой сколь угодно сложную сеть. В таком случае под выражением, приведенным выше, следует понимать сумму по всем ветвям, слагаемое же для каждой ветви является интегралом приведенного выше вида (контур интегрирования для каждой ветви может быть при этом незамкнутым).
§ В случае простого (не ветвящегося) контура (и при выполнении условий магнитостатического приближения, подразумевающих отсутствие накопления зарядов), ток I одинаков на всех участках контура и может быть вынесен за знак интеграла. (Это справедливо отдельно и для каждого неразветвленного участка разветвленной цепи).
Если же взять за точку отсчёта точку, в которой нужно найти вектор магнитной индукции, то формула немного упрощается:
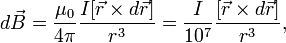
где 
- вектор описывающий кривую проводника с током ,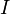 
- модуль , 
- вектор магнитной индукции, создаваемый элементом проводника 
.
Направление 
перпендикулярно плоскости, в которой лежат векторы 
и 
. Направление вектора магнитной индукции может быть найдено по правилу правого винта: направление вращения головки винта дает направление , если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора определяется выражением (в системе СИ)
Векторный потенциал даётся интегралом (в системе СИ)
