Энергия электромагнитного поля в лабораторной системе координат является положительно определенной величиной, то есть она положительна, если отлична от нуля хотя бы одна из компонент электромагнитного поля и обращается в ноль только в том случае, когда все компоненты электромагнитного поля равны нулю. Этот факт используется при доказательстве единственности решения различных задач для уравнений Максвелла. Рассмотрим пример.
Пусть уравнения Максвелла в лабораторном времени
, 
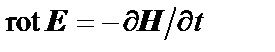(15)
решаются в области 
с границей 
, причем задано произвольное начальное условие при 
и одно из двух граничных условий:
(16)
где 
– единичный вектор в направлении нормали к поверхности .
Соотношение (13) может быть получено из уравнений (15) с однородной правой частью. Интегрируя (13) по области , пользуясь положительной определенностью плотности энергии легко показать, что однородная задача имеет только тривиальное решение, что и доказывает единственность решения задачи (15-16) с произвольными начальными данными.
Ситуация изменяется, если необходимо исследовать единственность решения задачи Гурса. Пусть начальное условие задано при 
. Выполним замену координат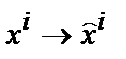 
, в результате чего уравнения (15) превратятся в уравнения (9). Вектор Пойнтинга и формулировка граничных условий не изменятся. Энергия преобразуется к виду
Положительная определенность такой конструкции не очевидна.
Рассмотрим ее более подробно. Эта величина неотрицательна. Действительно:
.
Определим условия на 
и 
, при которых 
равно нулю. Поскольку
,
искомые условия имеют вид:
. (17)
Заметим, что из (17) следует, что
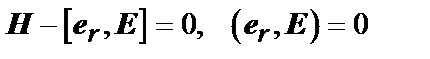. (18)
Подставим и , удовлетворяющие условиям (17) и (18), в уравнения Максвелла:
, 
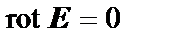. (19)
Заметим, что уравнения, содержащие дивергенции, обратятся в тождества типа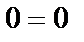 
.
Если 
, то представимо в виде градиента скалярной функции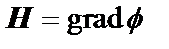 
, причем 
в силу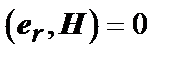 
. Из того, что 
следует 
. Значит, в шаре любого радиуса 
с центром в точке 
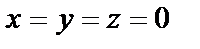скаляр 
является гармонической функцией и доставляет решение однородной задаче Неймана:
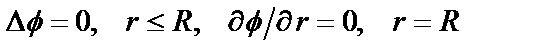. (20)
Задача (20) имеет своим решением произвольную функцию переменной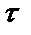 
, не зависящую от переменных 
[5]. В силу этого ее градиент, представляющий собой магнитное поле , равен нулю. Равенство нулю электрического поля следует из (17).
Таким образом, плотность энергии электромагнитного поля 
в координатах 
является величиной, положительно определенной на решениях уравнений Максвелла.
Если замена переменных имеет вид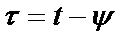 
, необходимо дополнительно потребовать, чтобы поверхности уровня 
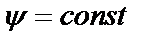были компактными. В частности, при замене 
, 
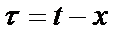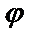может быть любой гармонической функцией переменных 
и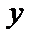 
.
СИЛА ЛОРЕНЦА - сила, действующая на заряженную частицу, движущуюся в электромагнитном поле. Ф-ла для с. Л. была впервые получена голландским физиком X. А. Лоренцом как результат обобщения опыта и имеет вид:
(в ВД- системы СГС). Здесь е - заряд, V - скорость частицы, В и H - векторы напряжённости электрич. поля и магн. индукции в той же системе отсчёта, в к-рой измеряется скорость V. Первый член в ф-ле Fэ - сила, действующая на заряженную частицу в электрич. поле, второй - в магнитном. Магнитная составляющая силы Лоренца Fm пропорциональна векторному произведению VxВ, т. е. она перпендикулярна векторам V и В. Следовательно, сила Fm не совершает механич. работы, а только искривляет траекторию движения частицы, не меняя её энергию. Величина магнитной составляющей
где альфа - угол между векторами V и В. Т. о., Fm максимальна, если направление движения частицы составляет с направлением магнитного поля прямой угол, и равна нулю, если частица движется вдоль направления поля.
В вакууме в постоянном однородном магн. поле, где В = Н, заряженная частица под действием Fm движется по винтовой линии с постоянной по величине скоростью V, при этом её движение складывается из равномерного прямолинейного движения вдоль направления магн. поля H (со скоростью, равной составляющей скорости частицы V в направлении Н и равномерного вращательного движения в плоскости, перпендикулярной Н (со скоростью Vn, равной составляющей V в направлении, перпендикулярном Н).
Проекция траектории частицы на плоскость, перпендикулярную Н, есть окружность радиуса r=cmVn/EH, а угловая частота вращения равна
(т. е. циклотронная, или гиромагнитная частота). Ось винтовой линии совпадает с направлением-Н, и центр окружности перемещается вдоль силовой линии поля.
Для релятивистских частиц с импульсом р
Если электрическое поле не равно нулю, то движение носит более сложный характер: наблюдается дрейф - перемещение центра вращения частицы перпендикулярно полю Н. Направление дрейфа определяется вектором ExH и не зависит от знака заряда. Скорость дрейфа и для простейшего случая скрещенных полей Е_|_H равна сЕ/Н. Дрейф проявляется и без электрического поля, если имеется др. сила (напр., сила тяжести) или если магнитное поле неоднородно.
13. Электрический диполь. Потенциал и поле диполя. Дипольное приближение для системы зарядов.
Совокупность двух равных по величине разноименных точечных зарядов q, расположенных на некотором расстоянии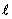 
друг от друга, малом по сравнению с расстоянием до рассматриваемой точки поля называется электрическим диполем.(рис.13.1)
Произведение 
называется моментом диполя. Прямая линия, соединяющая заряды называется осью диполя. Обычно момент диполя считается направленным по оси диполя в сторону положительного заряда.
Прежде чем заняться расчётом поля диполя, остановимся на общих моментах. Пусть, например, нас интересует гравитационное поле какого-то астероида неправильной формы. Поле в непосредственной близости от астероида можно получить только путём компьютерного расчёта. Но, чем дальше мы отходим от астероида, тем с большей точностью мы можем рассматривать его как материальную точку (поле которой мы знаем). При стремлении к большей математической строгости надо было сказать, что мы знаем асимптотическое поведение поля при 
С похожей ситуацией мы сталкиваемся и в электростатическом поле. Электростатическое поле по своим свойствам очень похоже на гравитационное (потому что аналогичны фундаментальные законы: закон Кулона и закон всемирного тяготения), но, если так можно сказать, «богаче» его. Ведь электрические заряды могут быть двух типов, между ними возможно и притяжение, и отталкивание, а между «гравитационными зарядами» (т.е. массами) возможно только притяжение.
Будем считать, что в какой-то ограниченной области распределены положительные и отрицательные точечные заряды q1, q2, …, qn. Полный заряд системы
(2)
Мы уже понимаем, что при Q ≠ 0 поле при больших r переходит в поле точечного заряда Q. Но возникает очень важный для нас вопрос: каким будет поле на больших расстояниях, если полный заряд
Q = 0? Самое простое распределение точечных зарядов с Q = 0 – это и есть диполь. Вот почему изучение поля диполя несёт в себе важные принципиальные моменты.
Итак, нас будут в основном интересовать такие ситуации, когда все характерные размеры r весьма велики по сравнению с расстоянием l между зарядами диполя. Эту ситуацию можно описать двояко. Во-первых, мы можем всегда иметь в виду, что заряды расположены на конечном расстоянии l друг от друга, и интересоваться поведением полученных решений при Но можно и п росто говорить о точечном диполе с определённым дипольным моментом p, тогда все наши результаты справедливы при любом r > 0 (две эти точки зрения, конечно, эквивалентны).
Мы будем использовать известные всем формулы для полей точечных зарядов и в полученных выражениях учитывать, что l мало. Поэтому напомним формулы приближённых вычислений: если 
, то 
Везде в выкладках знак «≈» будет указывать на то, что мы воспользовались этими формулами в случае малого параметра (малый параметр в рассматриваемых задачах – это l/r).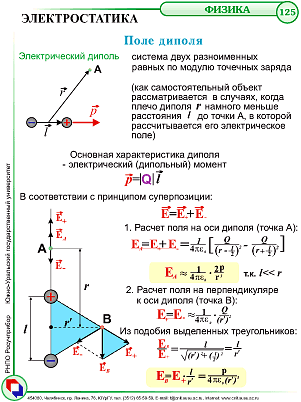 
В электростатике достаточное условие применимости дипольного приближения (в смысле задачи определения электрического потенциала или напряженности электрического поля, создаваемого системой зарядов, имеющей определенный суммарный заряд и определенный дипольный момент) описывается весьма просто: хорошим это приближение является для областей пространства, удаленных от системы-источника на расстояние r, много большее, чем характерный (а лучше — чем максимальный) размер d самой этой системы. Таким образом, для условий дипольное приближение r >> d является хорошим.
Если суммарный заряд системы равен нулю, а ее дипольный момент нулю не равен, дипольное приближение в своей области применимости является главным приближением, то есть в его области применимости оно описывает основной вклад в электрическое поле. Остальные же вклады при r >> d пренебрежимо малы (если только дипольный момент не оказывается слишком мал по сравнению с квадрупольным, октупольным или высшими мультипольными моментами).
Если суммарный заряд не равен нулю, главным становится монопольное приближение (нулевое приближение, закон Кулона в чистом виде), а дипольное приближение, являясь следующим, первым, приближением, может играть роль малой поправки к нему. Впрочем, в такой ситуации эта поправка будет очень мала в сравнении с нулевым приближением, если только мы находимся в области пространства, где вообще говоря само дипольное приближение является хорошим. Это несколько снижает его ценность в данном случае (за исключением, правда, ситуаций, описанных чуть ниже), поэтому главной областью применения дипольного приближения приходится признать случай нейтральных в целом систем зарядов.
Существуют ситуации, когда дипольное приближение является хорошим (иногда очень хорошим и в каких-то случаях даже может давать практически точное решение) и при невыполнении условия r >> d. Для этого нужно только чтобы высшие мультипольные моменты (начиная с квадрупольного) обращались в ноль или очень быстро стремились к нулю. Это довольно легко реализуется для некоторых распределенных систем.
В дипольном приближении, если суммарный заряд ноль, вся система зарядов, какой бы она ни была, если только ее дипольный момент не ноль, эквивалентна маленькому диполю (в этом случае всегда подразумевается маленький диполь) — в том смысле, что она создает поле, приближенно совпадающее с полем маленького диполя. В этом смысле любую такую систему отождествляют с диполем и к ней могут применяться термины диполь, поле диполя и т.д. В статье выше, даже если это не оговорено явно, всегда можно вместо слова диполь слова «нейтральная в целом система, имеющая ненулевой дипольный момент» — но, конечно, вообще говоря только в случае, если подразумевается выполнение условий корректности дипольного приближения.
Вектор электрической индукции в диэлектрике. Материальное уравнение для векторов электрической индукции. Диэлектрическая восприимчивость и диэлектрическая проницаемость вещества. Электрическое поле однородного политропного диалектрического шара.
Поляризационные заряды q' - это такие же обычные заряды, как и заряды q, и они также являются источником электрического поля. Поэтому теорема Гаусса для вектора напряженности электрического поля
E должна включать как сторонние, так и связанные заряды:
| EdS = 4n(q + q') (2.3.1)
S
Записывая теорему Гаусса в дифференциальной форме, имеем:
divE = 4к(р + р'), (2.3.2)
где q - сторонний заряд, р - плотность сторонних зарядов, q' - связанный заряд и р' - плотность связанных
зарядов. Эти формулы могут быть переписаны через вектор поляризации P, выразив связанные заряды через из формул (2.2.8) и (2.2.12) в предыдущего параграфа. IB дифференциальной форме имеем:
divE = -4%divP + 4кр (2.3.3)
div(E + 4kP) = 4 кр (2.3.4)
Или в интегральной форме получаем аналогично:
|(E + 4кР)dS = 4nq (2.3.5)
S
Введем новый вектор - вектор электрической индукции, или вектор электрического смещения, с помощью следующего соотношения:
D = E + 4кР (2.3.6)
Тогда уравнения (2.3.4) и (2.3.5) записываются в более короткой форме:
divD = 4кр
| DdS = 4щ (2-37)
S
Мы получили 1-ое уравнение системы уравнений Максвелла в дифференциальной и интегральной форме. Фактически эти уравнения представляют следующее: Поток вектора электрической индукции через любую замкнутую поверхность равен полному заряду сторонних носителей, находящихся внутри этой
поверхность. Таким образом, вектор D определяется только сторонними (свободными) зарядами. Уравнение (2.3.7) представляет собой обобщение теоремы Гаусса для электрического поля в веществе.
Свойства вещества сокрыты в векторе индукции электрического поля D, точнее, его связи с вектором
напряженности электрического поля E. Вектор D является искусственно введенным вектором поля, поскольку разделение зарядов на сторонние и связанные заряды условно (см Примечание 2).
Важно, что в вакууме вектор поляризации равен нулю P = 0 и вектор электрической индукции
совпадает с вектором напряженности электрического поля D = E.
Примечание 1: в системе СИ для вектора электрической индукции и теоремы Гаусса имеем:
D = е 0 E + P
divP = -р'; divE = — (р + р'); divD = р
е о
Примечание 2. Вектор электрической индукции (смещения) D, как и вектор поляризации P, является
искусственным вектором. Вектор D введен для того, чтобы выделить вклад сторонних зарядов в полное
электрическое поле. Вектор P введен для того, чтобы выделить вклад связанных зарядов в полное электрическое поле. Реальное поле, которое действует на пробные заряды, - есть напряженность
Для полного определения электромагнитного поля уравнения Максвелла необходимо дополнить материальными уравнениями, связывающими векторы 
и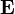 
(а также 
и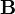 
) в веществе. В вакууме эти векторы совпадают, а в веществе связь между ними зачастую предполагают линейной:
Величины 
образуют тензор диэлектрической проницаемости. В принципе, он может зависеть как от точки внутри тела, так и от частоты колебаний электромагнитного поля. Визотропных средах тензор диэлектрической проницаемости сводится к скаляру, называемому также диэлектрической проницаемостью. Материальные уравнения для приобретают простой вид
Возможны среды, для которых зависимость между и 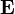является нелинейной (в основном — сегнетоэлектрики).
В вакууме поле характеризуется только одним вектором E - вектором напряженности электрического поля. В веществе, чтобы определять электрическое поле, действующее на пробные заряды, нужно еще знать
либо P, либо D. Поэтому полученное основное уравнение электростатики надо дополнять еще одним уравнением, которое могло бы связать между собой эти величины.
Принципиально возможно, зная атомную структуру вещества, рассчитать смещение электронов и ядер при включении внешнего электрического поля. Т.е. исходя из знания атомно-молекулярного строения,
можно в принципе вычислить вектор поляризации P и получить еще одно уравнение, связывающее
напряженность поля E внутри вещества и поляризацию. Однако универсальной зависимости P от вектора
напряженности E нет, для каждого вещества эта зависимость своя, поскольку атомы и молекулы обладают различными свойствами и по-разному реагируют на внешнее поле. Таким образом, на пути прямого
определения связи между векторами P и E возникают следующие трудности:
1) связь между векторами P и E не выражается простыми аналитическими формулами, и она не универсальна.
2) связь этих векторов рассчитать нелегко; только в последние годы делаются попытки теоретического расчета, применяя квантовую механику, благодаря развитию методов современной вычислительной физики.
Поэтому существует другой более простой путь, разработанный ранее, когда еще не существовало квантовой механики и четких представлений об атомно-молекулярной структуре веществ, - найти связь между поляризацией и электрическим полем в веществе эмпирическим путем. Опыт показывает, что связь
между векторами P и E для большинства диэлектриков линейна и однородна, в широком диапазоне внешних полей, но не приближающихся к внутриатомным полям. При этом необходимо отдельно рассматривать изотропные по пространственным свойствам диэлектрики и анизотропные. 1). Для изотропных диэлектриков и для не слишком больших внешних полей (меньших внутриатомных)
вектора E и P пропорциональны и коллинеарны:
P = aE (2.3.8)
Здесь коэффициент a - поляризуемость диэлектрика или диэлектрическая восприимчивость. Диэлектрическая восприимчивость определяется свойствами атомов и молекул вещества и может зависеть от плотности и температуры диэлектрика. Тогда подставляя (2.3.8) в вектор индукции (2.3.6), получаем:
D = E + 4лaE = (l + 4^a)E = sE (2.3.9)
Здесь мы ввели диэлектрическую проницаемость среды
S = 1 + 4ли. (2.3.10)
Этой величиной характеризуют индивидуальные свойства изотропных диэлектриков. Если рассматриваем
вакуум, то a = 0, s = 1 и D = E.
Примечание 3: в системе СИ имеем P = js0E; D = (s0 + js0)E = s0sE; s = 1 + х.
2). Анизотропные среды: например, кристаллы. Для них направления векторов E и P не совпадают, и поэтому связь между компонентами этих векторов осуществляется через более общую линейную зависимость:
| (2.3.12) |
P =Za jEj
(2.3.11)
Подробнее (2.3.11) можно переписать в виде:
P =a E +a E +a E
X XX x xy y xz z
P =a E +a E +a E
y yX X yy y yz z
P =a E +a E +a E
z zx X zy y zz z
Здесь а •• - безразмерные коэффициенты, зависящие от выбора координатных осей. Совокупность этих 9
У
коэффициентов |а iJ- j составляет тензор поляризуемости диэлектрика.
Аналогично имеем для связи векторов электрической индукции и электрической напряженности
| 8 ]] =5 ]] + 4ка ]] (2.3.14) |
D=Te,jE], (2.3.13)
|s j j - тензор диэлектрической проницаемости вещества:
8] =5] + 4к
Пользуясь законом сохранения энергии можно показать, что тензоры |а j j и j j симметричны, т.е.
где
а] =а i
(2.3.15)
8j =8 fi
Таким образом, в тензорах имеем 6 независимых величин - 6 компонент тензора диэлектрической
проницаемости j j. Основное физическое содержание соотношений (2.3.11)- (2.3.13) состоит в том, что
при включении внешнего электрического поля в общем случае смещение связанных зарядов и направление внутренних диполей происходит не в направлении приложенного поля, а под некоторым углом к нему. Вследствие этого суммарное электрическое поле внутри вещества становится не только другим по величине, но и по направлению.
В дальнейшем для простоты будем в основном говорить об изотропных диэлектриках.
Пусть незаряженный шар из диэлектрика радиусом R внесен во внешнее однородное поле, напряженность которого равна Е0.
Диэлектрическая проницаемость шара eш отлична от диэлектрической проницаемости среды eс(рис. 1.37). Поскольку как внутри шара, так и вне его нет свободных зарядов, то поле описывается уравнением Лапласа (1.12). Решение данного уравнения, записанного в сферической системе координат, проводят методом разделения переменных (методом Фурье). Поскольку это решение достаточно громоздко, то здесь приведем только окончательное выражение для потенциала внутри и вне шара.
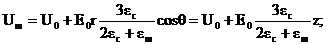
Здесь U0 – потенциал точки, находящейся в центре шара; z = r?cosq.
Напряженность поля внутри шара:
.
Таким образом, напряженность поля внутри шара направлена вдоль оси z и не зависит от координат точки. Это значит, что внутри шара поле однородно. Следовательно, шар поляризуется однородно.
Во внешнем пространстве электрическое поле искажается и около шара оно неоднородно и имеет две составляющие:
