Уравнения Максвелла для зарядов в вакууме, получаемые путем вариации функционала действия, представляют собой соотношения, связывающие компоненты тензора электромагнитного поля и 4-вектора плотности электрического тока. Тензор электромагнитного поля 
является кососимметричным тензором второго ранга типа 
. В лабораторной системе координат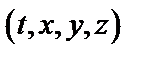 
, он имеет следующий вид [2]:
(1)
Наборы компонент 
и 
тензора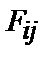 
составляют 3-векторы электрического 
и магнитного 
полей соответственно.
Лабораторные координаты в дальнейшем будем обозначать 
, 
. Введем координаты 
, соответствующие собственному времени:
, 
, 
, 
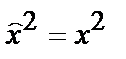. (2)
Рассмотрим 
– тензор электромагнитного поля в координатах 
:
(3)
Установим соответствие между компонентами тензоров 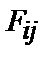и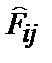 
. Для этого построим матрицы Якоби замены координат на 
:
, 
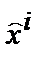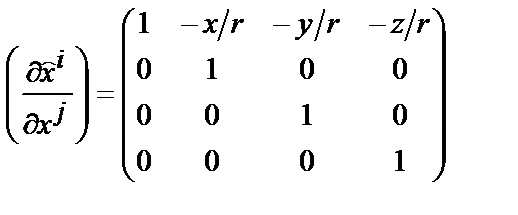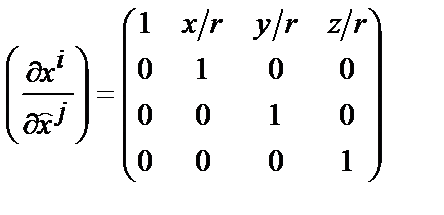, (4)
и вычислим явно, как преобразуется тензор электромагнитного поля [3]:
,
откуда
.
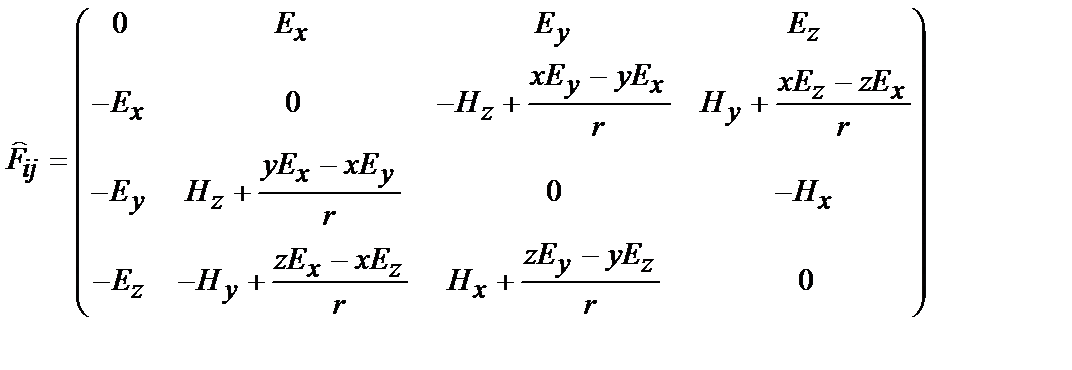Первая пара уравнений Максвелла в тензорном виде имеет следующий вид [2]:
(5)
Здесь операция 
– внешнее дифференцирование кососимметрического тензора
.
Эта операция является тензорной [4], то есть ее координатная запись не зависит от выбора системы координат. Поэтому
.
В силу этого первая пара трехмерных уравнений Максвелла в собственном времени:
,
где 
, 
, 
и 
обозначают дивергенцию и ротор в координатах 
, а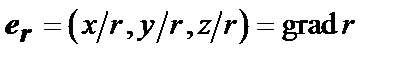 
.
Рассмотрим преобразование 4-вектора плотности электрического тока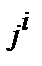 
при переходе (2) из координат в координаты 
. Пусть в координатах 
, где 
– плотность заряда, 
– 3-плотность электрического тока. Тогда в координатах 
. (6)
Вторая пара уравнений Максвелла с помощью тензора электромагнитного поля и 4-вектора плотности тока записывается в следующем виде:
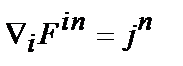, (7)
где 
обозначает ковариантное дифференцирование, а
,
где 
– метрический тензор в координатах ,
.
В координатах 
.
Ковариантное дифференцирование является тензорной операцией. Уравнение (7) в произвольных координатах имеет следующий вид:
, (8)
где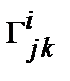 
– символы Кристоффеля.
Рассмотрим второе слагаемое в уравнении (8). Вычислим символы Кристоффеля в координатах 
[4]:
.
Среди всех комбинаций, возможных в правой части, только 
, 
, отличны от нуля. Во второе слагаемое (8) входят только те символы Кристоффеля вида 
, которые равны нулю. Третье слагаемое представляет собой свертку символов Кристоффеля, симметричных по нижним индексам 
с тензором, кососимметрическим по тем же индексам, поэтому оно равно нулю. Значит, в координатах 
уравнение (8) имеет вид:
Отсюда следует вторая пара трехмерных уравнений Максвелла:
,
где 
.
Таким образом, полная система уравнений Максвелла в собственном времени, то есть в координатах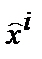 
имеет следующий вид:
,
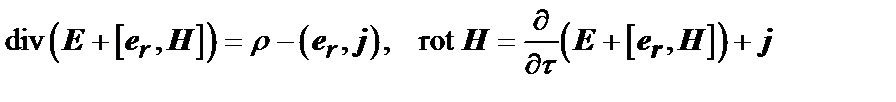