Электростатическая теорема Гаусса устанавливает математическую связь между потом вектора напряженности через замкнутую поверхность и зарядами, находящимися в объеме, ограниченном данной поверхностью.
Предположим, что имеется некоторый объем V, ограниченный поверхностью S и точечный заряд q внутри этого объема.
Рассмотрим поток N напряженности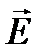 
сквозь эту поверхность.
. (5.1)
Так как q точечный заряд. То напряженность поля равна
, (5.2)
а значит
.
Учтем соотношение 
^ 
где 
- проекция площади элемента 
на плоскость, перпендикулярную радиус-вектору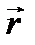 
, т.е. 
^ 
.
Рассмотрим сферу, на которой выделим площадку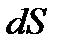 
и введем понятие телесного угла 
,который определим так:
. (5.3)
Для бесконечно малых величин справедливо соотношение: 
, и тогда из (5.1) с учетом (5.2) и (5.3) получаем:
(5.4)
Полный телесный угол, под которым видна замкнутая поверхность из точек внутри объема, равен 
(телесный угол измеряется в стерадианах: 1 стеррад = 
), а поток
(5.5)
Аналогичным образом можно посчитать поток 
сквозь замкнутую поверхность, если точечный заряд находится вне объема. В этом случае, как можно показать
. (5.6)
Объединяя (5.5) и (5.6) можно окончательно написать:
(5.7)
Утверждение, содержащееся в (5.7) и есть электростатическая теорема Гаусса для точечного заряда. Ее легко обобщить на случай, когда внутри объема находится или система точечных зарядов или непрерывно распределенный по объему заряд, используя принцип суперпозиции:
(5.8)
или
(5.9)
Физической основой теоремы Гаусса является закон Кулона, а значит теорема Гаусса является интегральной формулировкой закона Кулона.
Воспользуемся теоремой Остроградского-Гаусса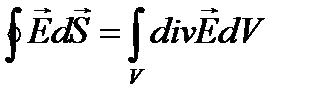 
и предположим, что в объеме V заряд распределен непрерывно с объемной плотностью 
, т.е. 
. Тогда 
, откуда легко найти, что
(5.10)
Ввиду произвольности объема, получаем:
(5.11)
Это и есть дифференциальная формулировка закона Кулона или уравнение Максвелла (1831-1879) для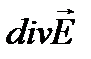 
.
