Система уравнений Максвелла как обобщение опытных данных. Ток проводимости и ток смещения. Взаимные превращения электрических и магнитных полей.
Между электрическими и магнитными полями существует глубокая внутренняя связь, проявляющаяся в том, что эти поля могут превращаться друг в друга. Всякое изменение магнитного поля всегда сопровождается появлением электрического поля и, наоборот, всякое изменение электрического поля приводит к появлению магнитного поля. Это взаимное превращение электрического и магнитного полей было открыто в начале второй половины прошлого века Максвелом, который развил общую теорию электромагнитного поля в покоящихся средах.
Ток смещения.
Постоянный ток не протекает в цепи с конденсатором, а в случае переменного напряжения в цепи ток протекает через конденсатор. Для постоянного тока конденсатор – разрыв в цепи, а для переменного этого разрыва нет. Поэтому необходимо заключить, что между обкладками конденсатора происходит некоторый процесс, который как бы замыкает ток проводимости. Этот процесс между обкладками конденсатора был назван током смещения. Напряженность поля между обкладками конденсатора 
. Из граничного условия для вектора 
следует, что диэлектрическое смещение между обкладками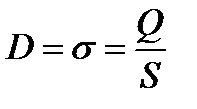 
, а сила тока в цепи равна 
. Тогда
, (25.1)
а значит процессом, замыкающим ток проводимости в цепи, является изменение электрического смещения во времени. Плотность тока
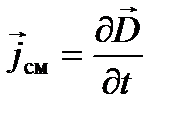. (25.2)
Существование тока смещения было постулировано Максвеллом в 1864 г. и затем экспериментально подтверждено другими учеными.
Почему скорость изменения вектора смещения называется плотностью тока? Само по себе математическое равенство величины 
, характеризующей процесс между обкладками конденсатора, т.е. равенство двух величин, относящихся к разным областям пространства и имеющим различную физическую природу, не содержит в себе, вообще говоря, какого-то физического закона. Поэтому называть ”током” можно только формально. Для того чтобы придать этому названию физический смысл, необходимо доказать, что обладает наиболее характерными свойствами тока, хотя и не представляет движения электрических зарядов, подобного току проводимости. Главным свойством тока проводимости является его способность порождать магнитное поле. Поэтому решающим является вопрос о том, порождает ли ток смещения магнитное поле так же, как его порождают ток проводимости, или, более точно, порождает ли величина (25.2) такое же магнитное поле, как равная ей объемная плотность тока проводимости? Максвелл дал утвердительный ответ на этот вопрос. Однако наиболее ярким подтверждением порождения магнитного поля током смещения является существование электромагнитных волн. Если бы ток смещения не создавал магнитного поля, то не могли бы существовать электромагнитные волны.
Уравнение Максвелла с током смещения.
Порождение магнитного поля токами проводимости описывается уравнением
(25.3)
Учитывая порождение поля током смещения, необходимо обобщить это уравнение в виде
(25.4)
Тогда, принимая во внимание (25.2), окончательно получаем уравнение
, (25.5)
являющееся одним из уравнений Максвелла.
Полученная в результате обобщения экспериментальных данных, эта система имеет вид:
Эти уравнения называются полевыми и справедливы при описании всех макроскопических электромагнитных явлений. Учет свойств среды достигается уравнениями
, (25.7)
называемыми обычно материальными уравнениями среды. Среды линейны, если 
и нелинейны если 
. Материальные уравнения, как правило, имеют вид функционалов.
Рассмотрим физический смысл уравнений.
Уравнение I выражает закон, по которому магнитное поле порождается токами проводимости и смещения, являющимися двумя возможными источниками магнитного поля. Уравнение II выражает закон электромагнитной индукции и указывает на изменяющееся магнитное поле как на один из возможных источников, порождающих электрическое поле. Вторым источником электрического поля являются электрические заряды (уравнение IV). Уравнение III говорит о том, что в природе нет магнитных зарядов.
Электромагнитное взаимодействие и его место среди других взаимодействий в природе. Электрический заряд. Микроскопические носители заряда. Опыт Милликена. Закон сохранения электрического заряда.
