Отношение эквивалентности

Важным видом бинарного отношения является отношение эквивалентности.

Определение 5.1. Бинарное отношение a на множестве X называется отношением эквивалентности на X, если a рефлексивно, симметрично и транзитивно.

Отношение эквивалентности часто обозначают символами ~, .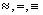

Примерами отношения эквивалентности служат:

· отношение тождества I_X = {(a, a) |a X } на непустом множестве X;

· отношение параллельности на множестве прямых плоскости;

· отношение подобия на множестве фигур плоскости;

· отношение равносильности на множестве уравнений;

· отношение "иметь одинаковые остатки при делении на фиксированное натуральное число m " на множестве целых чисел. Это отношение в математике называют отношением сравнимости по модулю m и обозначают a b (mod m);

· отношение "принадлежать одному виду" на множестве животных;

· отношение "быть родственниками" на множестве людей;

· отношение "быть одного роста" на множестве людей;

· отношение "жить в одном доме" на множестве людей.

Отношения "жить на одной улице", "быть похожими" на множестве людей отношениями эквивалентности не являются, так как не обладают свойством транзитивности.

Из перечисленных выше свойств бинарных отношений следует, что пересечение отношений эквивалентности является отношением эквивалентности.