При аэродинамических расчетах и изучении динамики движения самолетов используются различные системы координат. Чаще всего используются связанная, скоростная, нормальная и траекторная системы координат.
Связанная система координат 0 XYZ жестко связана с самолетом (отсюда ее название). Начало этой системы совпадает с центром масс самолета (см. рис. 18). Ось 0 X лежит в базовой плоскости самолета, она направлена в сторону носовой части и, как правило, параллельна САХ. Эта ось называется продольной осью. Ось 0 Y тоже лежит в базовой плоскости самолета, при этом она перпендикулярна оси 0 X и направлена к верхней части самолета. Она называется нормальной осью. Ось 0 Z перпендикулярна базовой плоскости самолета и направлена в сторону правого полукрыла. Эта ось называется поперечной осью.
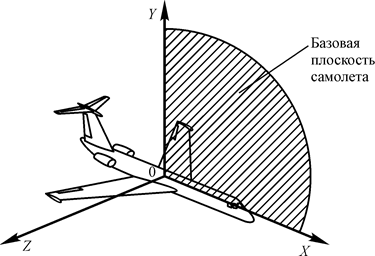
Рис. 18. Связанная система координат
Скоростная система координат 0 XaYaZa связана с вектором скорости движения центра масс самолета относительно воздушной среды 
(см. рис. 19), ее начало также помещают в центре масс самолета. Ось 0 Xa в скоростной системе координат всегда совпадает с вектором скорости и называется скоростной осью. Ось 0 Ya перпендикулярна вектору скорости, лежит в базовой плоскости самолета и направлена к верхней части самолета. Она называется осью подъемной силы. Ось 0 Za проводят так, чтобы она дополняла оси 0 Xa и 0 Ya до правой системы координат. Эта ось называется боковой осью.
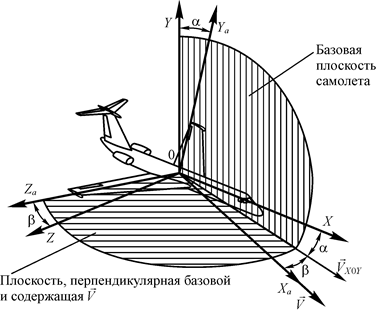
Рис. 19. Скоростная система координат
Для описания взаимного положения осей связанной и скоростной систем координат используются угол атаки и угол скольжения. Углом атаки a называется угол между осью 0 X связанной системы координат и проекцией вектора скорости на базовую плоскость самолета –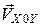 
. Углом скольжения b называется угол между вектором скорости и базовой плоскостью самолета. Легко заметить, что если скольжение отсутствует (b = 0), то определение угла атаки упрощается: угол a будет равен углу между продольной осью 0 X и вектором скорости .
Нормальная система координат 0 XgYgZg используется для описания пространственного положения самолета относительно поверхности Земли. Начало координат этой системы совпадает с началом связанной системы координат (см. рис. 20). Ось 0 Yg всегда направлена вверх по местной вертикали, а направление осей 0 Xg и 0 Zg выбирается в соответствии с решаемой задачей, при этом плоскость Xg 0 Zg всегда расположена горизонтально. Угол между осью 0 Xg и проекцией оси 0 X на горизонтальную плоскость XXg 0 Zg называется углом рыскания и обозначается y. Угол между продольной осью 0 X и горизонтальной плоскостью Xg 0 Zg называется углом тангажа и обозначается j. Угол между поперечной осью 0 Z и горизонтальной плоскостью Xg 0 Zg называется углом крена и обозначается g.
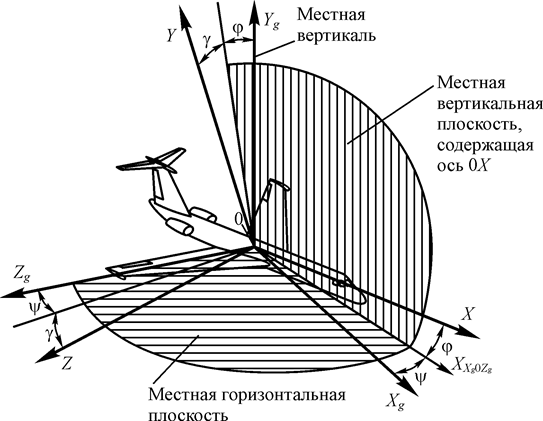
Рис. 20. Нормальная система координат
Траекторная система координат 0 X к Y к Z к используется главным образом в динамике полета для описания движения самолета относительно поверхности Земли. В общем случае скорость полета относительно воздушной среды может не совпадать со скоростью полета относительно Земли, т.к. в реальной атмосфере почти всегда имеется движение воздушных масс, проще говоря, ветер. Ветер оказывает воздействие на самолет, и суммарная скорость его движения относительно поверхности Земли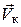 
(земная скорость) будет равна:
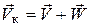, (31)
где – скорость самолета относительно воздушной среды;
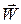– скорость ветра относительно Земли.
Траекторная система координат связана с вектором земной скорости 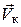. Начало координат этой системы совпадает с началом связанной системы координат (см. рис. 21). Ось 0 X к совпадает с направлением вектора земной скорости 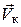. Ось 0 Y к размещается в вертикальной плоскости, проходящей через ось 0 X к, и направлена вверх от Земли. Ось 0 Z к образует правую систему координат. Траекторная система координат может быть получена из нормальной путем поворота последней на угол пути x и угол наклона траектории q.
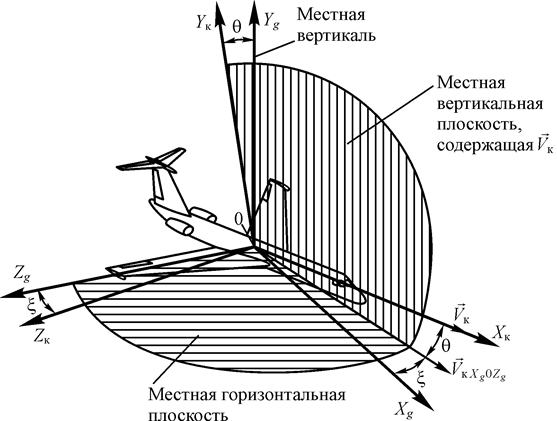
Рис. 21. Траекторная система координат
Углом пути x называется угол между проекцией вектора 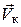на горизонтальную плоскость Xg 0 Zg и осью 0 Xg. Угол наклона траектории q – это угол между вектором земной скорости 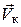и местной горизонтальной плоскостью Xg 0 Zg.
