Основы кинематики и динамики воздуха

 

В аэродинамике при изучении движения воздуха иногда удобнее использовать не модель сплошной среды, а модель, рассматривающую среду как совокупность множества частиц. В этой модели движение частиц представляют в виде траекторий и линий тока. Траекторией движения частицы называется геометрическое место точек, в которых частица находилась в процессе своего движения. При этом вектор скорости частицы во всех точках траектории направлен по касательной к ней (см. рис. 4). Линия тока – это линия, составленная из точек, в которых движущиеся частицы находятся в фиксированный момент времени, причем векторы скоростей частиц направлены по касательной к этой линии так же, как и в случае с траекторией. Траектория и линия тока различаются тем, что траектория описывает движение одной частицы в разные моменты времени, а линия тока – движение совокупности частиц в каждый фиксированный момент времени. При определенном условии траектория и линия тока совпадают. Это происходит в том случае, если в каждой фиксированной точке линии тока вектор скорости не изменяется с течением времени по величине и направлению. Такое течение называется установившимся. При неустановившемся течении вектор скорости со временем изменяется, что приводит к изменению формы линии тока и она уже не совпадает с траекторией движения отдельной частицы.

 

 

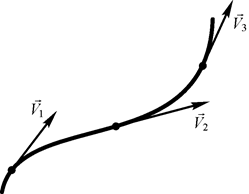
Рис. 4. Траектория частицы

 

Представим себе замкнутую линию и через точки этой линии проведем линии тока. В результате получим замкнутую поверхность, образованную линиями тока. Такая поверхность называется трубкой тока. Поскольку, как следует из определения линии тока, векторы скорости движения частиц направлены по касательной к поверхности трубки тока, то эта поверхность является непроницаемой для частиц воздуха. Воздух, движущийся внутри трубки тока называется струйкой. Струйка называется элементарной, если ее поперечное сечение достаточно мало и можно считать, что в каждый фиксированный момент времени скорости частиц воздуха в этом сечении равны. Рассмотрим такую струйку (см. рис. 5).

 

 

 

Рис. 5. Элементарная струйка

 

Поскольку поверхность трубки тока непроницаема для частиц воздуха, то при установившемся течении через каждое поперечное сечение элементарной струйки в единицу времени будет протекать одна и та же масса воздуха. Это вытекает из закона сохранения массы, если принять, что трубка тока не имеет разрывов, через которые может поступать или уходить воздух. Поэтому формула, описывающая это явление, называется уравнением неразрывности и имеет вид:

 

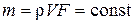, (10)

где m – масса воздуха, протекающего через поперечное сечение струйки в единицу времени;

r – плотность воздуха в данном сечении струйки;

V – скорость воздуха в данном сечении струйки;

F – площадь поперечного сечения струйки.

 

Для малых скоростей течения (при М < 0,3) можно принять, что воздух несжимаем, т.е. плотность воздуха не меняется от сечения к сечению (r = const). Тогда ее можно исключить из уравнения (10) и, возвращаясь к рис. 5, записать:

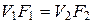. (11)

 

Из этого уравнения можно сделать важный вывод: при уменьшении площади поперечного сечения струйки скорость течения воздуха в ней возрастает, а при увеличении – падает. Но это справедливо только для дозвуковых течений (М < 1). При сверхзвуке (М > 1) картина меняется с точностью до наоборот. Здесь уже важную роль играет сжимаемость. Например, при уменьшении площади поперечного сечения плотность воздуха увеличивается настолько, что в целом произведение F r возрастает, а это приводит к уменьшению скорости потока V (см. формулу (10)). Поэтому при сверхзвуковом потоке для того, чтобы увеличить скорость, необходимо также увеличивать площадь поперечного сечения струйки.

Важное место в аэродинамике отводится также закону сохранения энергии, который используется для получения взаимосвязи давления и скорости воздуха в струе. На рис. 6 показана струйка при виде сбоку. Рассмотрим относительно некоторого уровня баланс энергии масс воздуха, проходящих через сечения 1 и 2 за одинаковый промежуток времени D t. Движение воздуха в струйке будем считать установившимся, а сжимаемость и трение учитывать не будем. Выделим для рассмотрения некоторую массу воздуха m, проходящую через сечение 1 со скоростью V ₁ за время D t. Эта масса обладает кинетической энергией, равной 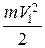и имеет потенциальную энергию, равную работе силы тяжести mgh ₁. Кроме этого, на рассматриваемую массу воздействует сила давления воздуха p ₁ F ₁, лежащего выше сечения 1, поэтому необходимо также учесть работу, совершаемую этой силой. Работа, как известно, равна произведению силы на перемещение, которое в данном случае можно вычислить, умножив скорость V ₁ на промежуток времени D t, в течение которого рассматриваемая масса воздуха проходит через сечение 1. Согласно закону сохранения суммарная энергия рассматриваемой массы воздуха при прохождении ею сечения 2 не изменится, поэтому можно записать:

. (12)

 

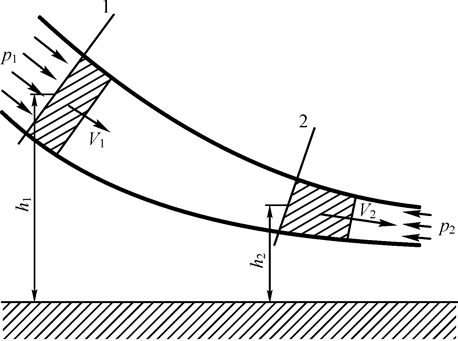
Рис. 6. Движение воздуха в струйке

 

В соответствии с уравнением (11) объем воздуха, проходящий через сечение 1 должен быть равен объему воздуха, проходящего через сечение 2:

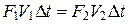. (13)

Поделим уравнение (12) на уравнение (13) и получим:

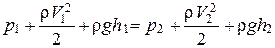. (14)

Или:

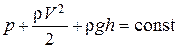. (15)

Мы получили уравнение Бернулли для газа без учета сжимаемости. Если пренебречь действием силы тяжести или предположить, что движение воздуха происходит в горизонтальной плоскости, то потенциальная энергия рассматриваемой массы воздуха не изменится, и из выражения (15) произведение r gh можно исключить:

. (16)

Слагаемое p называется статическим давлением, а слагаемое – динамическим давлением (или скоростным напором). Сумма же статического и динамического давлений называется полным давлением и обозначается p ₀:

. (17)

При внимательном рассмотрении уравнения Бернулли можно заметить, что при увеличении скорости потока динамическое давление будет расти, а статическое соответственно падать, т.к. их сумма изменяться не должна. Так, при обтекании тела набегающим потоком воздуха (см. рис. 7) на его носке существует точка А (критическая точка), в которой скорость потока из-за полного торможения равна 0. В этой точке динамическая составляющая равна нулю, а статическое давление максимально и равно полному давлению. В любой другой точке поверхности тела скорость потока будет больше 0, а это значит, что статическое давление будем меньше, чем в критической точке.

 

 

Рис. 7. Обтекание тела набегающим потоком

 

Взаимосвязь статического и динамического давлений хорошо иллюстрируется на примере функционирования прибора, который носит название трубка Пито – Прандтля, или в технике – приемник воздушного давления (ПВД). Этот прибор широко используется в авиации для определения скорости полета. Схематично трубка Пито – Прандтля изображена на рис. 8. Прибор имеет две полости, соединенных с манометром. Когда трубка выставлена вдоль вектора скорости набегающего потока, то в полости 1 давление воздуха будет равно полному давлению, т.к. это критическая точка и поток в ней полностью тормозится. Полость 2 сообщается с потоком через боковое отверстие в трубке, при этом линии тока проходят мимо этого отверстия, не искажаясь. За счет этого в полости 2 действует только статическое давление, а влияние динамического давления исключено. Разность давлений в полостях 1 и 2, измеряемая с помощью манометра, будет равна скоростному напору:

. (18)

Отсюда, зная плотность воздуха, легко определить скорость набегающего потока (или скорость полета).

 

 

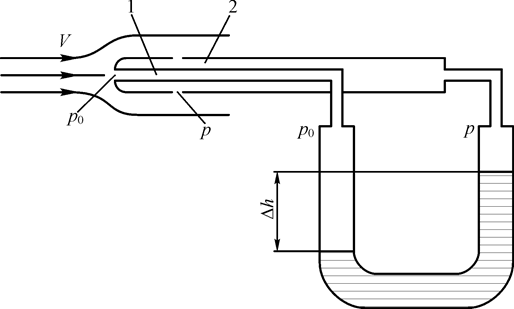
Рис. 8. Схема трубки Пито-Прандтля