Определите силу тока в неразветвленной части цепи и напряжение на клеммах источника, если 
, ток через катушку равен 10 А, ток в ветви, содержащей конденсатор и резистор – 14,1 А.
Решение
1. Резистор и конденсатор соединены последовательно, значит, токи в этих элементах цепи одинаковые 
. Катушка включена параллельно ветви RC, следовательно, одинаковы напряжения 
.
2. Построение векторной диаграммы начнем с тока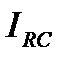 
- расположим его горизонтально. Напряжение на активной нагрузке 
совпадает с током по фазе, следовательно, вектор 
на диаграмме будет параллелен вектору тока 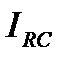. Напряжение на емкостной нагрузке 
отстает от тока по фазе на 
.
По условию 
. При последовательном соединении напряжения на участках с одинаковым сопротивлением тоже равны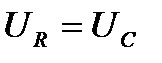 
. На диаграмме вектора и имеют одинаковую длину. Нетрудно видеть, что сдвиг по фазе между током 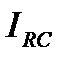и напряжением 
равен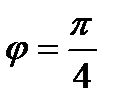 
.
3. На индуктивной нагрузке ток отстает по фазе от напряжения на . По условию ток в катушке больше, чем в ветви с конденсатором, поэтому вектор 
на диаграмме длиннее вектора .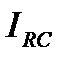
4. Ток в неразветвленной части цепи 
складывается из токов в ветвях 
и 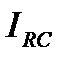. Сложение нужно произвести с учетом фазовых сдвигов, для этого нужно сложить вектора и 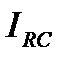на векторной диаграмме. Задача упрощается, если вектор предварительно разложить на две составляющих, как показано на рисунке:
5. Из векторной диаграммы нетрудно видеть, что 
.
6. Составляющие тока равны: 
и
.
7. Очевидно, что ток в неразветвленной части цепи равен
10. Опять о мощности в цепи переменного тока
Как мы только что показали, конденсатор и катушка не потребляют энергию от источника за период. Остается предположить, что преобразование электрической энергии безвозвратно в тепловую энергию происходит исключительно за счет наличия в цепи активной нагрузки.
Рассмотрим знакомый пример – последовательное соединение R,L, и С.
Векторная диаграмма для такой цепи нам уже знакома:
Выделим отдельно треугольник напряжений:
Мощность, потребляемая цепью, равна:
Из треугольника напряжений нетрудно видеть, что
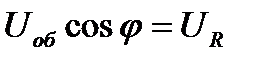
Тогда для мощности, потребляемой всей цепочкой, имеем
Что и требовалось доказать.
Важно, что наш вывод верен для любого вида соединения. Преобразование электрической энергии в цепи переменного тока в тепловую энергию происходит только на активной нагрузке!
Кстати, тогда для расчета мощности, потребляемой всей цепью не обязательно находить общий ток, общее напряжение и сдвиг фаз между ними. Достаточно воспользоваться законом Джоуля-Ленца для каждого резистора, входящего в состав цепи:
Введем еще ряд важных понятий.
Вернемся опять к последовательной цепи с активной нагрузкой, индуктивностью и емкостью. Умножим все стороны треугольника напряжений на значение тока в цепи (он во всех элементах цепи одинаков). Получим подобный треугольник, каждая сторона которого имеет размерность мощности.
Вводят следующие обозначения
Полную мощность S иначе называют кажущейся, т.е. такой, которую мог бы дать источник, если бы не было сдвига по фазе между током и напряжением. Единицы измерения полной мощности [S] = [В×А].
Реактивная мощность Q – это та энергия, которой в течение периода цепь обменивается с источником. Ее измеряют в Вольт-Амперах реактивных (Вар).
Только активная мощность Р соответствует электрической энергии, используемой для преобразования в тепло, для получения механической работы и т.д.
Почему нужно стремиться, чтобы коэффициент мощности был как можно больше?
Низкие значения cosj порождают значительные дополнительные потери на нагревание подводящих проводов, обмоток генератора. Покажем это.
Пусть одинаковые мощности передаются от одинаковых генераторов двум нагрузкам с cosj0=1 и cosj<1.
Мощность, расходуемая на нагревание проводов, по закону Джоуля -Ленца будет равна
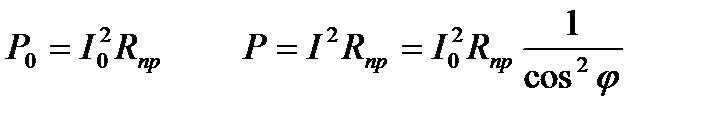
Результат очевиден.
