Емкостная нагрузка в цепи переменного тока
1. Рассчитайте сопротивление конденсатора емкостью С = 0,1 мкФ переменному току, если частота тока а) 50 Гц; б) 1000 Гц; в) 10 кГц. Постройте график зависимости емкостного сопротивления от частоты переменного тока.
2. К городской сети переменного тока с напряжением Uэф = 127 В присоединен конденсатор емкостью С = 40 мкФ. Определите амплитудное значение тока в цепи.
3. К зажимам генератора присоединен конденсатор емкостью С = 0,1 мкФ. Определите амплитуду напряжения на зажимах генератора, если амплитуда тока Imax = 2,2 А, а частота тока n = 5 кГц.
4. Найдите емкость конденсатора, если амплитуда переменного напряжения на нем U0 =120 В, действующее значение тока I = 0,86 А, частота тока n = 50 Гц.
Индуктивная нагрузка в цепи переменного тока
1. Индуктивность катушки L = 0,5 мГн. Рассчитайте сопротивление катушки переменному току, если его частота а) 50 Гц; б) 1000 Гц; в) 10 кГц. Постройте график зависимости индуктивного сопротивления от частоты переменного тока. Катушка идеальная.
2. Найдите индуктивность катушки, если амплитуда переменного напряжения на ее концах Uмах = 160 В, амплитуда тока в ней Iмах = 10 А и частота тока 50 Гц. Катушка идеальная.
3. Индуктивное сопротивление катушки ХL = 500 Ом, эффективное напряжение в сети, в которую включена катушка, Uэф = 100 В, частота тока 1000 Гц. Определите индуктивность катушки и амплитудное значение тока в цепи. Активным сопротивлением катушки и подводящих проводов пренебречь.
Указания:
1. Помним, что для расчета емкостного или индуктивного сопротивления необходимо знать циклическую частоту w, а не обычную частоту n. Связь между ними w = 2pn.
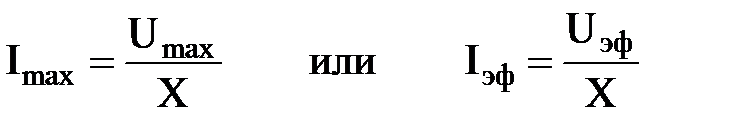
2. Закон Ома для цепи с катушкой или конденсатором можно записать как для амплитудных, так и для действующих (эффективных) значений тока и напряжения.
Нельзя применять закон Ома, если значение одной из величин (тока или напряженяе) действующее, а значение другой величины амплитудное!!!
3. Действующие и амплитудные значения тока и напряжения связаны между собой следующим образом
Действующее и эффективное значение тока или напряжения – это одно и то же! Можно обозначать так, как Вам больше нравится – возможны три варианта:
7. Последовательное соединение R, L, C.
Рассмотрим реальный колебательный контур с источником синусоидальной ЭДС. Задача заключается в определении тока, протекающего по цепи.
Задачу можно решить двумя способами: алгебраически и геометрически. Обратимся сначала к алгебраическому решению. Запишем для контура второй закон Кирхгофа – сумма падений напряжений вдоль замкнутого контура равна сумме ЭДС, действующих в контуре:
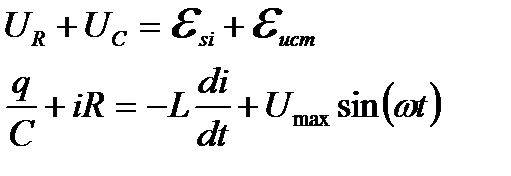
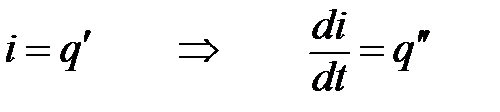С учетом того, что
уравнение перепишется в виде
Введем привычные обозначения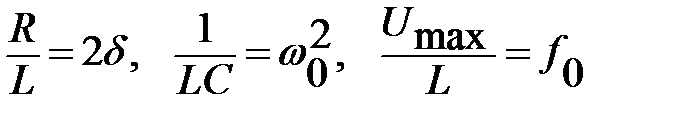 
. Тогда дифференциальное уравнение примет вид 
.
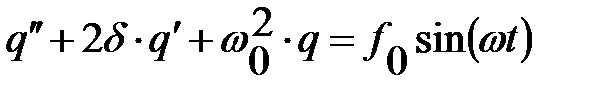С подобным дифференциальным уравнением мы уже сталкивались, рассматривая вынужденные механические колебания под действием синусоидальной внешней вынуждающей силы. Тогда же мы показывали, что решение уравнения ищется в виде 
.
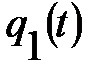- решение однородного дифференциального уравнения имеет вид 
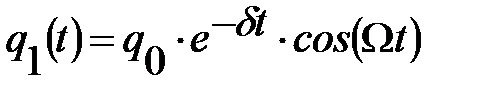, где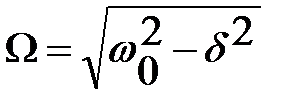 
. С физической точки зрения это означает, что включение переменного тока сопровождается «звоном» собственных колебаний контура, затухающих с течением времени. Время затухания собственных колебаний будет порядка времени релаксации 
.
Если же мы, как обычно в электротехнике, интересуемся установившимися колебаниями при 
>> 
, то, как было уже показано ранее решение дифференциального уравнения ищется в виде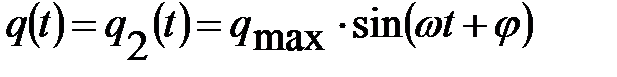 
. Физический смысл решения заключается в том, что под действием синусоидальной ЭДС в контуре будут происходить гармонические колебания с частотой внешней ЭДС. Очевидно, что мгновенные значения тока в контуре и напряжения на клеммах генератора сдвинуты по фазе, а это означает, что закон Ома для мгновенных значений тока и напряжения не выполняется.
В силу математической тождественности дифференциальных уравнений вынужденных механических и вынужденных электрических колебаний
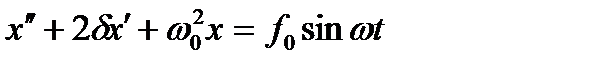
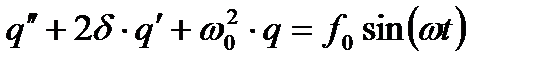
мы можем воспользоваться уже готовым результатом, проведя замену механических величин на соответствующие электрические. Тогда
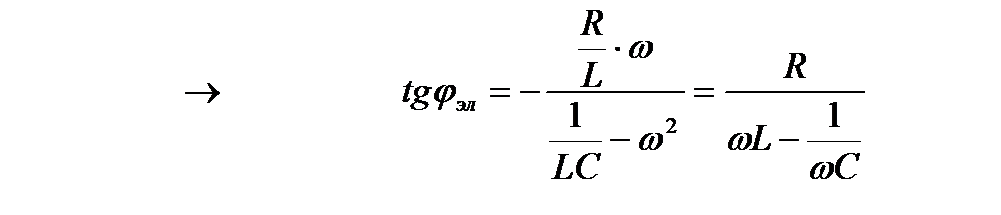
Ток к цепи равен 
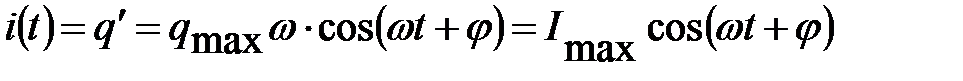, где
Амплитуда тока в контуре прямо пропорциональна амплитуде напряжения, то есть для амплитудных значений тока и напряжения выполняется закон Ома.
Величина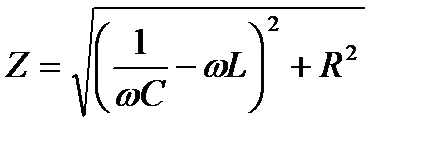 
играет роль сопротивления последовательной 
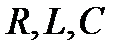-цепи. Такое «сопротивление» принято называть импедансом.
Выше найден сдвиг фаз между зарядом и напряжением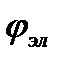 
, а поскольку колебания тока опережают колебания заряда на 
, то сдвиг фаз между током и напряжением будет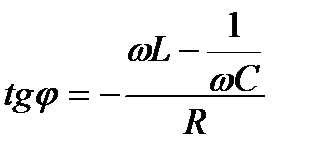 
.
Итак, поставленная задача решена. Мы показали, что под действием синусоидальной ЭДС в колебательном контуре происходят гармонические колебания тока, нашли амплитуду тока и сдвиг по фазе между током и напряжением. Для последовательной 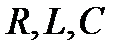-цепи можно пользоваться готовыми формулами. Однако, как правило, цепи переменного тока бывают не только последовательными. В этих случаях полученный нами результат не годится. В этих случаях гораздо проще рассчитать цепь графически, а не алгебраически. Покажем, как это делается.
При последовательном соединении сила тока одинакова во всех участках цепи, следовательно, 
. Если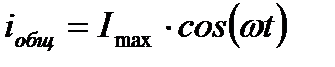 
, то колебания напряжения на активной нагрузке 
совпадают по фазе с колебания ми силы тока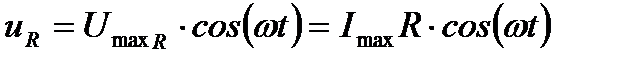 
.
На емкостной нагрузке колебания напряжения отстают от тока на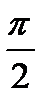 
: 
.
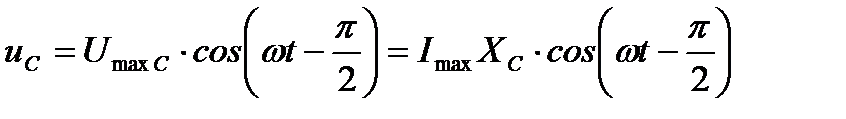На индуктивной нагрузке напряжение опережает ток на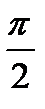 
: 
.
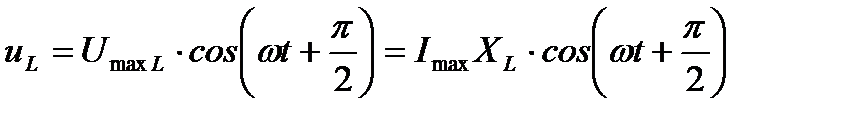Мгновенное значение общего напряжения при последовательном соединении равно сумме напряжений на отдельных участках
Для сложения гармонических функций одинаковой частоты удобно воспользоваться методом векторных диаграмм. Каждое колебание изображается вектором, которому в полярных координатах соответствуют модуль (амплитуда) и полярный угол (фаза).
Изобразим вектор тока горизонтально. Напряжение на активной нагрузке 
синфазно току, соответственно откладываем вектор 
параллельно вектору тока. Напряжение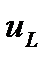 
опережает ток на 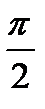, соответственно откладываем вектор 
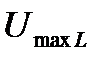перпендикулярно току с опережением по фазе. Напряжение 
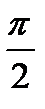отстает от тока на , откладываем вектор 
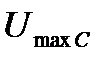перпендикулярно току с отставанием по фазе.
На диаграмме, как правило, опускают индексы «max», чтобы не загромождать рисунок.
Сумма всех трех векторов напряжений даст вектор общего напряжения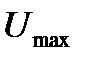 
. Нетрудно видеть, что между током и напряжением существует сдвиг по фазе, это значит, что между мгновенными значениями тока и напряжения пропорциональность отсутствует. Для мгновенных значений тока и напряжения закон Ома не выполняется!
Сдвиг по фазе между напряжением и током
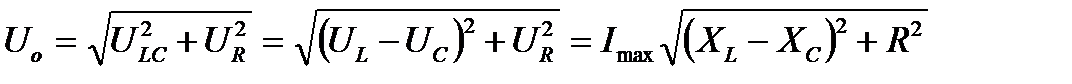Амплитуда общего напряжения 
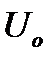равна
Опять-таки обнаруживаем пропорциональность между амплитудными значениями тока и напряжения, это значит, что для них выполняется закон Ома.
8. Резонанс напряжений (резонанс в последовательной 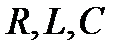-цепи)
Предположим, что при заданной амплитуде напряжения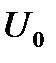 
на клеммах генератора мы будем варьировать частоту 
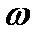внешней ЭДС. Очевидно, что амплитуда силы тока 
будет меняться, ибо индуктивное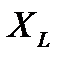 
и емкостное 
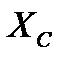сопротивления зависят от частоты .
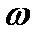Нетрудно видеть, что амплитуда тока примет максимальное значение при услови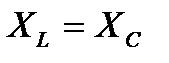и 
или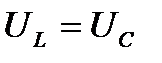 
. В этом случае наблюдается резонанс. При последовательном соединении элементов он называется резонансом напряжений. Векторная диаграмма при резонансе выглядит следующим образом
Напряжения на индуктивном и емкостном сопротивлениях равны по модулю и колеблются в противофазе, следовательно, они компенсируют друг друга. Общее напряжение становится равным падению напряжения на активной нагрузке.
Часто параметры контура подбираются таким образом, что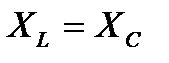 
>> . Тогда 
>> 
. При резонансе напряжений напряжения на отдельных участках цепи (на емкости и индуктивности) могут значительно превосходить напряжение на клеммах генератора.
Сдвиг по фазе между током и общим напряжением при резонансе обращается в ноль. При резонансе колебательный контур ведет себя как цепь исключительно с активной нагрузкой.
Частота тока, при которой наблюдается резонанс, может быть найдена следующим образом:
Как и следовало ожидать, резонанс наблюдается при совпадении частоты генератора с собственной частотой колебательного контура.
Резонансная кривая выглядит следующим образом
9. Резонанс токов
Рассмотрим параллельное соединение конденсатора с катушкой. Поскольку реальная катушка обладает активным сопротивлением, эквивалентная электрическая цепь будет выглядеть следующим образом:
Задача остается прежней – зная приложенное напряжение, рассчитать ток в цепи.
При параллельном соединении напряжения на ветвях, содержащих конденсатор и катушку, одинаковые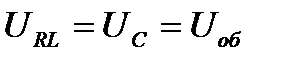 
. Ток в неразветвленной части 
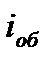(его мы и хотим определить) делится на два тока 
.
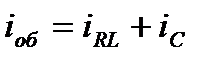Для расчета этой цепи удобнее воспользоваться методом векторных диаграмм.
Начнем с ветви, содержащей индуктивность и активное сопротивление.
Напряжение на активной нагрузке совпадает по фазе с током – на векторной диаграмме вектор 
сонаправлен вектору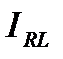 
.
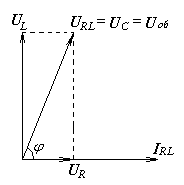Напряжение на индуктивной нагрузке опережает ток на 
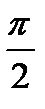- строим вектор 
перпендикулярно вектору тока с опережением по фазе. Общее напряжение находим по правилу параллелограмма. Оно опережает ток в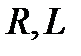 
-ветви на 
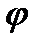радиан.
Сопротивление 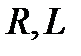-ветви равно 
. Амплитуда тока в этой ветви может быть найдена по закону Ома 
, а сдвиг по фазе 
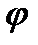определим по чертежу 
.
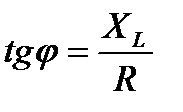Разложим ток в 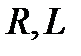-ветви на две составляющих – активную 
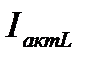, параллельную вектору напряжения, и 
, перпендикулярную вектору напряжения:
Теперь перейдем к построению векторной диаграммы для всей цепи. Поскольку напряжение на отдельных ветвях одинаково, в основу диаграммы положим вектор общего напряжения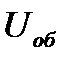 
, расположив его горизонтально.
Ток в ветви, содержащей емкость, найдем по закону Ома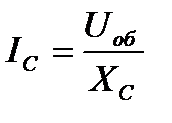 
. Этот ток опережает напряжение по фазе на 
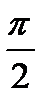и колеблется в противофазе с . Ток в неразветвленной части цепи может быть найден по теореме Пифагора:
Нетрудно видеть, что при выполнении условия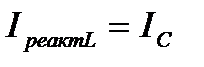 
ток в неразветвленной части цепи принимает минимальное значение, равное 
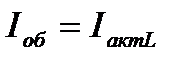. При этом токи в ветвях 
и 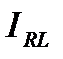могут оказаться намного больше тока в неразветвленной части цепи, при этом они колеблются практически в противофазе. В этом случае мы имеем дело с так называемым резонансом токов. Векторная диаграмма для резонанса токов выглядит следующим образом
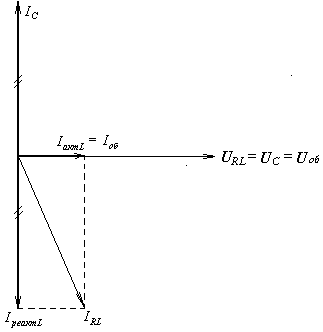
При резонансе токов цепь ведет себя так, как будто в ней содержится только активная нагрузка. Аналогичная ситуация наблюдалась и при резонансе напряжений.
Найдем резонансную частоту
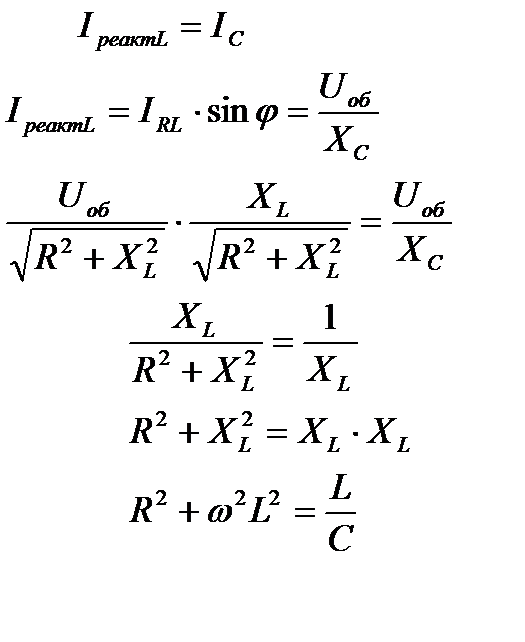
Тогда резонансная частота равна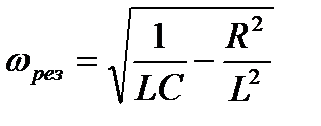 
. Как правило, активное сопротивление катушки много меньше ее индуктивного сопротивления. В этом случае
т.е. резонанс токов наблюдается при совпадении частоты внешней ЭДС с собственной частотой колебательного контура.
Резонанс токов широко используется в радиотехнике, например, в приемном колебательном контуре антенны, в автогенераторе. В электротехнике резонанс токов используется для повышения коэффициента мощности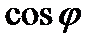 
.
