 Активной нагрузкой в цепи переменного тока называется такой участок, на котором вся электрическая энергия необратимо преобразуется в тепловую. В роли активной нагрузки может быть обычный резистор (лампа накаливания, электронагревательный элемент и т.д.)
Активной нагрузкой в цепи переменного тока называется такой участок, на котором вся электрическая энергия необратимо преобразуется в тепловую. В роли активной нагрузки может быть обычный резистор (лампа накаливания, электронагревательный элемент и т.д.)
Пусть напряжение на концах участка цепи, являющегося активной нагрузкой, меняется по гармоническому закону  .
.
 Чтобы вся электрическая энергия необратимо преобразовывалась в тепловую энергию, необходимо, чтобы мгновенная мощность в любой момент времени была положительной, а это возможно только при
Чтобы вся электрическая энергия необратимо преобразовывалась в тепловую энергию, необходимо, чтобы мгновенная мощность в любой момент времени была положительной, а это возможно только при  . Следовательно, для активной нагрузки напряжение и сила тока колеблются в одной фазе.
. Следовательно, для активной нагрузки напряжение и сила тока колеблются в одной фазе.

Нетрудно видеть, что мгновенные значения силы тока 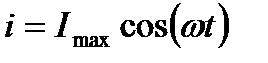 и напряжения
и напряжения  пропорциональны друг другу. Это утверждение – не что иное, как закон Ома для участка цепи:
пропорциональны друг другу. Это утверждение – не что иное, как закон Ома для участка цепи:
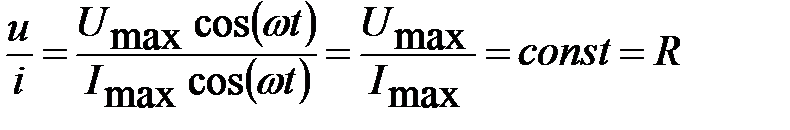
 Таким образом, на активной нагрузке закон Ома выполняется как для мгновенных, так и для амплитудных значений.
Таким образом, на активной нагрузке закон Ома выполняется как для мгновенных, так и для амплитудных значений.
При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться амплитудными или мгновенными значениями токов и напряжений, а их средние значения за период равны нулю.
Наиболее удобным оказалось введение так называемых действующих значений тока и напряжения. В основу этих понятий положено тепловое действие тока.
Действующее значение переменного тока – это значение постоянного тока, при протекании которого по цепи в проводнике выделяется за период столько же теплоты, сколько и при протекании переменного тока.
 Тепло, выделяемое в резисторе при протекании по нему постоянного тока, может быть найдено из закона Джоуля –Ленца:
Тепло, выделяемое в резисторе при протекании по нему постоянного тока, может быть найдено из закона Джоуля –Ленца:
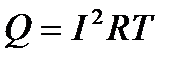
Тепло  , выделяемое переменным током в том же сопротивлении R за малое время
, выделяемое переменным током в том же сопротивлении R за малое время  , может быть выражено через мгновенное значение тока
, может быть выражено через мгновенное значение тока  :
:

 Тепло, выделяемое за период, находим суммированием малых
Тепло, выделяемое за период, находим суммированием малых  :
:

 Приравняв (*) и (**), найдем действующее значение переменного тока:
Приравняв (*) и (**), найдем действующее значение переменного тока:
 Выражения для действующих значений ЭДС и напряжения выглядят аналогично:
Выражения для действующих значений ЭДС и напряжения выглядят аналогично:
В соответствии с ГОСТом действующие значения тока, напряжения и ЭДС обозначаются соответствующими прописными буквами без индексов.
Электроизмерительные приборы переменного тока градуируют в действующих значениях измеряемых величин.
 5. Емкостная нагрузка в цепи переменного тока.
5. Емкостная нагрузка в цепи переменного тока.
Конденсатор в цепи переменного тока представляет так называемую емкостную нагрузку. Наличие диэлектрика между обкладками конденсатора приводит к тому, что постоянный ток не может течь по участку цепи, содержащему конденсатор. В цепи переменного тока ситуация меняется: под действием переменной ЭДС конденсатор может заряжаться и разряжаться, в этом случае по участку цепи, содержащему конденсатор, протекает ток зарядки или разрядки.
Наша задача – выяснить, как меняется ток зарядки и разрядки конденсатора, если его подключить к источнику синусоидальной ЭДС  .
.
Очевидно, что напряжение на конденсаторе совпадает с напряжением на клеммах генератора  . Тогда заряд на конденсаторе
. Тогда заряд на конденсаторе

Поскольку ток зарядки конденсатора – не что иное, как производная от заряда на конденсаторе по времени, получаем:

Воспользуемся формулами приведения:

Видим, что ток в цепи, содержащей конденсатор, меняется по гармоническому закону с частотой переменной ЭДС. Однако, фазы напряжения на конденсаторе и тока отличаются. Ток опережает напряжение на конденсаторе на 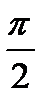 .
.


Сравнивая графики зависимостей тока и напряжения от времени, нетрудно увидеть, что пропорциональность между мгновенными значениями тока и напряжения отсутствует. Иными словами, закон Ома для мгновенных значений тока и напряжения не выполняется!
 Вернемся к зависимости тока от времени
Вернемся к зависимости тока от времени
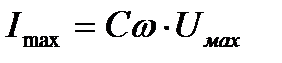 Величина, стоящая перед знаком косинуса, - амплитудное значение тока
Величина, стоящая перед знаком косинуса, - амплитудное значение тока
Максимальное значение тока в цепи с конденсатором прямо пропорционально максимальному значению напряжения. Это означает, что для амплитудных значений тока и напряжения выполняется закон Ома.
Коэффициент пропорциональности 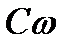 - проводимость участка цепи, содержащего конденсатор. Тогда величина
- проводимость участка цепи, содержащего конденсатор. Тогда величина  играет роль сопротивления, его называют емкостным сопротивлением.
играет роль сопротивления, его называют емкостным сопротивлением.
Емкостное сопротивление зависит не только от емкости конденсатора, но и от частоты тока  .С увеличением частоты тока сопротивление конденсатора падает, а амплитуда тока при этом, наоборот, увеличивается. Таким образом, конденсатор хорошо «пропускает» ток высокой частоты и плохо – низкой. Сопротивление конденсатора становится бесконечно большим, если частота тока
.С увеличением частоты тока сопротивление конденсатора падает, а амплитуда тока при этом, наоборот, увеличивается. Таким образом, конденсатор хорошо «пропускает» ток высокой частоты и плохо – низкой. Сопротивление конденсатора становится бесконечно большим, если частота тока  , то есть постоянный ток не может течь через участок, содержащий конденсатор (как это уже было сказано ранее).
, то есть постоянный ток не может течь через участок, содержащий конденсатор (как это уже было сказано ранее).

Коэффициент мощности для участка цепи, содержащего конденсатор, равен нулю  , следовательно, участок цепи, содержащий конденсатор, не потребляет энергию от сети. Точнее, мгновенная мощность в цепи с конденсатором меняет знак через каждые четверть периода. Четверть периода конденсатор заряжается, потребляя энергию от источника, на этом этапе мгновенная мощность положительна. Следующую четверть периода конденсатор разряжается, возвращая энергию источнику, при этом мгновенная мощность отрицательна.
, следовательно, участок цепи, содержащий конденсатор, не потребляет энергию от сети. Точнее, мгновенная мощность в цепи с конденсатором меняет знак через каждые четверть периода. Четверть периода конденсатор заряжается, потребляя энергию от источника, на этом этапе мгновенная мощность положительна. Следующую четверть периода конденсатор разряжается, возвращая энергию источнику, при этом мгновенная мощность отрицательна.
Роль емкостного сопротивления, таким образом, сводится к ограничению силы тока в цепи, содержащей конденсатор.






