42. Вероятность выигрыша по одному билету лотереи равна 0,05. Найти математическое ожидание M (2 X -0,5), если случайная величина X равна числу выигрышных билетов среди 15 купленных.
43. Ветеринар в зоопарке обследует 5 жирафов. Вероятность того, что рост жирафа будет больше 6 метров, равна 0,1. Найти дисперсию D (2 X -4), если случайная величина X равна числу обследованных жирафов с ростом более 6 метров.
44. Найти математическое ожидание M (2 X +3), если случайная величина X принимает целые неотрицательные значения от 0 до 5 с вероятностями:
 .
.
45. Случайная величина X распределена по нормальному закону с параметрами 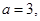
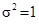 . Укажите значения вероятностей в соответствующих клетках таблицы:
. Укажите значения вероятностей в соответствующих клетках таблицы:
| 0,0017 | 0,5 | 0,7054 | 0,9973 | |||
P (X  3) = 3) =
| ||||||
| P (X < 3,54) = | ||||||
| P (X = 6) = | ||||||
| P (X < 100) = |
46. Длина анаконды описывается случайной величиной X, распределенной по нормальному закону, причем P (X >10) = 0,5. Найти математическое ожидание M (5 X -6).
47. Длина переднего рога у африканского белого носорога описывается случайной величиной X, распределенной по нормальному закону с параметрами a =0,8 и 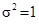 . Найти дисперсию D (5 X -0,8).
. Найти дисперсию D (5 X -0,8).
48. Найти математическое ожидание M (5 X -7), если случайная величина X распределена по нормальному закону, и график ее плотности имеет вид:

49. Найти дисперсию D (4 X –3), если плотность случайной величины X имеет вид:

50. Найти дисперсию D (3-2 X), если случайная величина X распределена по закону Пуассона с параметром 
Закон больших чисел
51. Под наблюдением ветеринара в зоопарке находится 300 животных. Вероятность того, что в течение дня животному потребуется помощь, равна 0,1. С помощью неравенства Чебышева оценить вероятность того, что число вызовов, поступивших в течение дня, отклонится от своего среднего значения более чем на 6 (по абсолютной величине).
Ответы: 1) 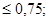 2)
2) 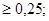 3)
3) 
52. Вероятность изготовления нестандартной линзы равна 0,2. Пользуясь неравенством Чебышева, оценить вероятность того, что доля нестандартных линз в партии из 10000 штук отличается от вероятности изготовления таких линз более чем на 0,05 (по абсолютной величине).
Ответы: 1)  2)
2)  3)
3) 
53. В данной местности среднее значение скорости ветра у земли равно 4 м/сек. Используя лемму Чебышева, оценить вероятность того, что в заданный день скорость ветра при одном наблюдении не превысит 16 м/сек.
Ответы: 1)  2)
2)  3)
3) 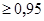 .
.
Выборочный метод
54. Найти несмещенную оценку генеральной средней, если данные, полученные в результате повторной выборки объема 50, представлены в табл. 3.
| Табл. 3 | Табл. 4 | |||||||||

| 
| |||||||||

| 
| 
|
55. Найти несмещенную оценку генеральной доли значений признака, которые не превосходят 40, если данные, полученные в результате бесповторной выборки объема 100, представлены в табл. 4.
56. Найти состоятельную оценку генеральной дисперсии, если в результате повторной выборки получены следующие данные: 

57. Построить доверительный интервал, в котором с вероятностью 0,9545 заключена генеральная доля, если по результатам повторной выборки объема 100 получена выборочная доля 
Ответы: 1) (0,05; 0,95); 2) (0,1; 0,5); 3) (0,4; 0,6); 4) (0,1; 0,9).
58. Как изменится доверительный интервал, если объем выборки оставить прежним, а доверительную вероятность уменьшить?
Ответы: 1) увеличится; 2) уменьшится; 3) не изменится.
59. Как нужно изменить объем выборки, чтобы тот же доверительный интервал гарантировать с большей вероятностью?
Ответы: 1) увеличить; 2) уменьшить; 3) оставить прежним.
60. Какие из перечисленных величин являются неслучайными величинами?
Ответы: 1) выборочная доля; 2) генеральная доля;
3) выборочная дисперсия; 4) генеральная средняя.
9. Элементы теории корреляции
61. В задачах были вычислены коэффициенты регрессии  и
и  . В каких задачах допущены ошибки?
. В каких задачах допущены ошибки?
Ответы: 1)  = – 0,3 и
= – 0,3 и  = – 1,5; 2)
= – 1,5; 2)  = 3,21 и
= 3,21 и  = 0,18;
= 0,18;
3)  = – 0,25 и
= – 0,25 и  = 2,67; 4)
= 2,67; 4)  = 0,3 и
= 0,3 и  = 5.
= 5.
62. На рисунках изображены прямые регрессии с коэффициентами корреляции | r | = 0,3 и | r | = 0,8. Какой рисунок соответствует коэффициенту корреляции r = - 0,8.
Ответы:
1)  2)
2) 
3)  4)
4) 
63. Найти среднее значение признака Y, если прямые регрессии для признаков Y и X изображены на рисунке:

64. При исследовании корреляционной зависимости между объемом производства X и доходами от реализации продукции Y получены следующие уравнения регрессии: y = 0,3 x + 120 и x = 1,6 y – 88. Найти выборочный коэффициент корреляции между величинами X и Y.
Ответы: 1) 0,48; 2) 0,69; 3) – 0,69; 4) - 0,49.
65. При исследовании корреляционной зависимости между удоем коров X и потреблением концентратов Y, получены следующие данные:  = 10 л/день,
= 10 л/день,  = 2 кг/день,
= 2 кг/день, 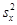 = 6,
= 6,  = 0,5,
= 0,5,  =1,5. Используя соответствующее уравнение регрессии, найти средний удой коров при потреблении 3 кг концентратов в день.
=1,5. Используя соответствующее уравнение регрессии, найти средний удой коров при потреблении 3 кг концентратов в день.
66. При исследовании зависимости между потребляемой предприятием электроэнергией X (млн. кВт. ч) и производимой продукцией Y (млн. руб.) получены следующие данные:  =10,
=10,  =4,
=4,  =0,8,
=0,8,  =0,5. Найти выборочный коэффициент корреляции.
=0,5. Найти выборочный коэффициент корреляции.
Ответы: 1) 0,63; 2) 0,4; 3) 0,6; 4) 0,3.
Типовой вариант теста
1. Посажено восемь семян. Обозначим через X число взошедших семян. Пусть событие A состоит в том, что число взошедших семян не более трех. С какими из перечисленных ниже событий событие A совместимо?
Ответы: 1) (X = 1); 2) (X = 3); 3) (X = 4); 4) (X = 7).
2. Пусть A – случайное событие, найти 
Ответы: 1)  2)
2)  3) 0; 4) 1.
3) 0; 4) 1.
3. При игре в карты пользуются колодой из 36 карт. Какова вероятность того, что первой сданной картой будет не карта масти «пик»?
4. Вероятности попадания в цель при стрельбе из трех орудий равны соответственно 0,7, 0,8 и 0,5. Какова вероятность того, что первое и второе орудия промахнулись?
5. Подбросили две игральные кости. Рассмотрим два события: A – «сумма выпавших очков более 10», B – «сумма выпавших очков равна 12». Найти условную вероятность PA (B).
Ответы: 1) 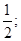 2)
2) 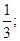 3)
3)  4) 1.
4) 1.
6. Известно, что 90% выпускаемой продукции соответствует стандарту. Упрощенная схема контроля признает пригодной стандартную продукцию с вероятностью 0,9 и нестандартную с вероятностью 0,2. Определить вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту.
Ответы: 1) 0,83; 2) 0,98; 3) 0,17; 4) 0,81.
7. Предположим, что вероятность выловить рыбу при одной поклевке равна 0,7. Какова вероятность того, что рыбак поймает хотя бы одну рыбу, если у него четыре поклевки?
8. При каком значении параметра b функция распределения непрерывной случайной величины имеет вид:

9. В урне 2 красных и 3 зеленых шара. Из урны извлекают шары до тех пор, пока не появится зеленый. Пусть случайная величина X равна числу извлеченных шаров. Укажите значения вероятностей в соответствующих клетках таблицы:
| 0,1 | 0,2 | 0,3 | 0,4 | 0,6 | ||
| P (X =0) = | ||||||
| P (X =1) = | ||||||
| P (X =2) = | ||||||
| P (X =3) = |
10. Найти математическое ожидание случайной величины X, если ее плотность имеет вид:

Ответы: 1) 1; 2) 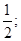 3)
3)  .
.
11. Найти дисперсию D (2 X -3), если случайная величина X принимает целые неотрицательные значения с вероятностями:
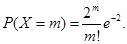

12. Ежедневный расход цемента на стройке – случайная величина, математическое ожидание которой равно 20 т, а среднее квадратическое отклонение 3 т. Оценить с помощью неравенства Чебышева вероятность того, что в ближайший день расход цемента на стройке отклонится от математического ожидания не более чем на 4 т (по абсолютной величине).
Ответы: 1)  2)
2) 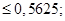 3)
3) 
13. Вычислить доверительную вероятность для оценки генеральной средней значения признака, если предельная ошибка выборки  , а по результатам повторной выборки объема 100 получена выборочная средняя
, а по результатам повторной выборки объема 100 получена выборочная средняя  и дисперсия
и дисперсия 
14. Как связаны между собой средние квадратические отклонения выборочных средних для повторной  и бесповторной
и бесповторной  выборок, если объем генеральной совокупности очень велик?
выборок, если объем генеральной совокупности очень велик?
Ответы: 1)  2)
2) 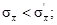 3)
3) 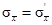 .
.
15. Установить направление и тесноту связи между случайными величинами, если их коэффициент корреляции r = – 0,21.
Ответы: 1) прямая; 2) обратная; 3) тесная; 4) слабая.
16. При исследовании корреляционной зависимости между объемом производства X и доходами от реализации продукции Y получены следующие уравнения регрессии: y = 0,3 x + 120 и x = 1,6 y – 88. Найти среднее значение величины Y.
ЛИТЕРАТУРА
Основная
1. Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: ЮНИТИ, 2000, 2001, 2003, 2004, 2007.
Дополнительная
2. Войтенко М.А. Руководство к решению задач по теории вероятностей. – М.: ВЗФЭИ, 1988.
3. Кремер Н.Ш., Путко Б.А., Тришин И.М. Математика для экономистов: от Арифметики до Эконометрики. / Под ред. Н.Ш. Кремера. – М.: Высшее образование, 2007.
4. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов, ч. 2. – М.: Высшая школа, 1982.
5. Кремер Н.Ш. Математическая статистика. – ВЗФЭИ. М.: Экономическое образование, 1992.
6. Четыркин Е.М., Калихман И.Л. Вероятность и статистика. М.: Финансы и статистика, 1982.
Ответы
1. 3. 2. 1. 3. 1; 2. 4. 1; 3; 4. 5. 1; 3. 6. 2. 7. 0,6. 8. 0,8. 9. 0,2. 10. 2. 11. 3. 12. 0,05. 13. 0,44. 14. 1. 15. 3. 16. 4. 17. 0,5. 18. 4. 19. 0,35. 20. 2. 21. 1. 22. 0,00015. 23. 0. 24. 3. 25. 0,9502. 26. 0,0916. 27. 0,0036. 28. 0,1. 29. 1; 4; 6. 30. 1; 6. 31. 2; 5. 32. P (X =0)=0,6; P (X =1)=0; P (X =2)=0,2; P (X =3)=0,2. 33. 0,4. 34. 3. 35. F (-2)=0; F (0)=0,1; F (2,5)=0,5; F (5)=0,5. 36. 0,9. 37. P (X =0)=0,3; P (X =1)=0,5; P (X =2)=0,2; P (X =3)=0. 38. P (X =0)=0; P (X =1)=0,3; P (X =2)=0,6; P (X =3)=0,1. 39. 3,2. 40. 0,81. 41. 0,3375. 42. 1. 43. 1,8. 44. 4. 45. P (X ³3)=0,5; P (X <3,54)=0,7054; P (X =6)=0; P (X <100)=1. 46. 44. 47. 25. 48. 8. 49. 16. 50. 8. 51. 1. 52. 3. 53. 1. 54. 200. 55. 0,2. 56. 25. 57. 3. 58. 2. 59. 1. 60. 2; 4. 61. 3; 4. 62. 4. 63. 10. 64. 1. 65. 13. 66. 2.






