Классификация событий
1. Пусть A – случайное событие. Чему равно событие  ?
?
Ответы: 1) A; 2)  3) достоверное событие; 4) невозможное событие.
3) достоверное событие; 4) невозможное событие.
2. Если наступление одного события исключает наступление другого, то события называются:
Ответы: 1) несовместными; 2) совместными;
3) независимыми; 4) зависимыми.
3. В урне 4 черных и 3 белых шара. Наудачу вынимают один шар. Пусть событие A состоит в том, что вынули белый шар, а событие B – вынули черный шар. Какие из следующих утверждений верны?
Ответы: 1) события A и В несовместны; 2) события А и В противоположны; 3) события А и В равновозможны; 4) события А и В независимы.
4. Число X выбирают наудачу из множества {1, 2, 3, 4}. Укажите, какие из перечисленных событий составляют полную группу событий.
Ответы: 1) A = (X = 1); 2) B = (X = 2); 3) C = (X = 3);
4) D – «число X делится на 2»; 5) E – «X – простое число».
Классическое определение вероятности, основные теоремы
5. Какими из перечисленных свойств не могут обладать события A и B, если их вероятности равны соответственно 0,6 и 0,3.
Ответы: 1) образуют полную группу событий; 2) несовместны;
3) противоположны; 4) совместны.
6. Если наступление события B влечет за собой наступление события A, то P (A×B) равна:
Ответы: 1)  2)
2)  3) 0; 4) 1.
3) 0; 4) 1.
7. Вероятности событий A и B равны соответственно 0,3 и 0,4. Чему равна вероятность их суммы, если вероятность их произведения 0,1?
8. В зоопарке два страуса из 6 имеют рост более 2,5 м. На выездную выставку случайным образом выбирают трех страусов. Какова вероятность того, что среди них хотя бы один с ростом более 2,5 м?
9. В урне 4 красных, один белый и один синий шар. Из урны извлекают три шара, не возвращая их обратно. Найти вероятность того, что извлеченные шары будут разных цветов.
10. Игральную кость подбросили один раз. Какова вероятность того, что выпадет не менее пяти очков?
Ответы: 1) 1; 2) 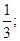 3)
3)  4)
4) 
11. На шести карточках написаны буквы А, В, К, М, О, С. После перемешивания вынимают наугад одну карточку за другой и раскладывают по порядку. Найти вероятность того, что при этом получится слово «МОСКВА»
Ответы: 1)  2)
2)  3)
3)  4)
4) 
12. Некто забыл последние две цифры телефонного номера, но помнит, что они нечетные и различные. Какова вероятность того, что он сразу наберет нужный номер, если будет набирать эти цифры случайно?
13. Первый стрелок попадает в цель с вероятностью 0,6, а второй с вероятностью 0,8. Каждый стрелок сделал по одному выстрелу. Какова вероятность того, что один из них промахнулся?
14. Бросают две игральные кости. Найти вероятность того, что в сумме выпадет 11 очков.
Ответы: 1) 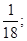 2)
2)  3)
3) 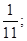 4)
4) 
Условные вероятности
15. Игральную кость подбросили один раз. Рассмотрим два события: A – «выпало четное число очков», B – «выпало 3 очка». Найти условную вероятность PA (B).
Ответы: 1) 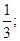 2)
2)  3) 0; 4) 1.
3) 0; 4) 1.
16. В урне 5 белых и 3 черных шара. Из урны извлекают последовательно два шара. Рассмотрим два события: A – «первый извлеченный шар – белый», B – «второй извлеченный шар черный». Найти условную вероятность PA (B).
Ответы: 1) 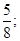 2)
2) 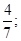 3)
3)  4)
4) 
17. Монету подбросили два раза. Рассмотрим два события: A – «выпали два орла», B – «второй раз выпал орел». Найти условную вероятность PB (A).
18. Подбросили две игральные кости. Рассмотрим два события: A – «сумма выпавших очков менее 4», B – «сумма выпавших очков равна 3». Найти условную вероятность PA (B).
Ответы: 1)  2)
2)  3) 0; 4) 1.
3) 0; 4) 1.
19. В группе 4 отличника, 10 хорошо успевающих и 6 занимающихся слабо студентов. На предстоящем экзамене отличники могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся студенты могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. На экзамен наугад приглашается один студент. Какова вероятность того, что он получит хорошую оценку?
20. В обувную мастерскую для ремонта приносят сапоги и туфли в соотношении 2:3. Вероятность качественного ремонта для сапог равна 0,9, а для туфель 0,85. Какова вероятность того, что отобранная для проверки пара отремонтирована качественно?
Ответы: 1) 0,42; 2) 0,87; 3) 0,78; 4) 0,75.
21. На сборку поступают детали с двух автоматов. Первый дает в среднем 2% брака, второй 3% брака. Найти вероятность того, что наугад взятая бракованная деталь изготовлена вторым автоматом, если с первого автомата поступило 1000 деталей, а со второго 2000.
Ответы: 1) 0,75; 2) 0,5; 3) 0,18; 4) 0,25.






