Федеральное агентство по образованию
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Всероссийский заочный финансово – экономический институт
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Методические указания
по компьютерному тестированию
Для самостоятельной работы студентов II курса всех специальностей и слушателей факультета непрерывного обучения
(первое высшее образование)
Москва – 2007
Федеральное агентство по образованию
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Всероссийский заочный финансово – экономический институт
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Методические указания
по компьютерному тестированию
для самостоятельной работы студентов I курса всех специальностей и слушателей факультета непрерывного обучения
(первое высшее образование)
Факультет менеджмента и маркетинга
Кафедра высшей математики
Москва – 2007
Методические указания подготовлены доц. Эйсымонт И.М. при авторском участии и под общей редакцией проф. Кремера Н.Ш.
Учебно – методическое издание одобрено на заседании Научно-методического совета ВЗФЭИ
Проректор, председатель НМС, профессор Д.М. Дайитбегов
В методическом пособии рассматриваются вопросы организации компьютерного тестирования, приводятся основные типы и примеры тестовых заданий, типовой вариант теста по дисциплине «Теория вероятностей и математическая статистика».
Для студентов второго курса и слушателей факультета непрерывного образования.
© Всероссийский заочный
финансово – экономический
институт (ВЗФЭИ), 2007.
Предисловие
Для совершенствования внутривузовской системы контроля качества подготовки специалистов по математическим дисциплинам существенное значение приобретает компьютерное тестирование студентов, позволяющее в условиях ограниченных ресурсов провести контроль уровня подготовки студентов на различных этапах обучения.
Компьютерное тестирование – одна из форм контроля качества подготовки наряду с традиционными формами, такими как выполнение контрольных или курсовых работ, сдача зачетов и т.п. Достоинством тестирования является возможность независимой оценки подготовки студентов на базе единой базы тестовых заданий. Это позволяет рассматривать компьютерное тестирование как удобный независимый индикатор уровня подготовки студентов.
Цель настоящего методического пособия – оказать помощь студентам второго курса и слушателям факультета непрерывного обучения по подготовке к компьютерному тестированию по дисциплине «Теория вероятностей и математическая статистика».
В пособии рассматриваются вопросы организации компьютерного тестирования, приводятся основные типы и примеры тестовых заданий, типовой вариант теста, выбранных из тестовой базы кафедры высшей математики.
Следует отметить, что компьютерное тестирование, с учетом его ограниченных возможностей и специфики, не может заменить полноценного курсового экзамена по математической дисциплине. Поэтому учебная деятельность студента должна быть нацелена на завершающий этап обучения по данной дисциплине – курсовой экзамен, а компьютерное тестирование следует рассматривать как один из этапов подготовки к такому экзамену.
Общие вопросы
Компьютерное тестирование проводится по всем темам дисциплины «Теория вероятностей и математическая статистика». Часть заданий – это теоретические вопросы, а часть – практические задания.
Как правило, студент проходит тестирование после того, как прослушан лекционный курс и проведены практические занятия, выполнены контрольные работы № 3 и № 4 и пройдены собеседование по ним. Расписание проведения тестирования устанавливается территориальным подразделением (филиалом).
Для сдачи компьютерного тестирования студенту необходимо явиться в компьютерный класс со студенческим билетом или зачетной книжкой. Для выполнения тестовых заданий студенту необходимо иметь бумагу, ручку и калькулятор. Таблицы значений функций Гаусса, Лапласа и Пуассона (Кремер Н.Ш., Теория вероятностей и математическая статистика, М.: ЮНИТИ, 2000-2005, таблицы I, II и III из Приложений) предоставляются организаторами тестирования.
Время тестирования один час (60 минут) с момента получения первого тестового задания.
По результатам тестирования компьютером выставляется оценка. Если оценка положительная, то преподаватель проставляет в зачетную книжку студента зачет. Студентам, получившим при компьютерном тестировании оценку «неудовлетворительно», необходимо пройти тестирование повторно. К повторному тестированию студенты допускаются не ранее, чем через три дня после получения неудовлетворительной оценки. Студенты, получившие при тестировании оценку «неудовлетворительно» трижды, проходят устное собеседование по его результатам с преподавателем, после чего выставляется окончательная оценка.
К экзамену допускаются студенты, которые успешно прошли собеседования по двум контрольным работам и получили зачет по компьютерному тестированию.
Основные типы тестовых заданий
1. Вопрос открытого типа: «текстовая строка».
Вопросы этого типа требуют вычисления точного ответа (без округления) в виде целого числа без знаков препинания: «5», «-5», либо в виде десятичной дроби через запятую, например, 0,9987. При этом предполагается, что если аргументы функций Гаусса и Лапласа больше 4, то соответственно 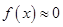 и
и 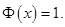
Пример 1. Всхожесть семян составляет 90%. Найти вероятность того, что из 400 посеянных семян взойдет не менее 360. Ответ: 0,5.
Пример 2. Студент Иванов посещает лекции по математике с вероятностью 0,8, студент Петров с вероятностью 0,9, хотя бы один из них присутствует на каждой лекции. Какова вероятность того, что они встретились на лекции? Ответ: 0,7.
2. Вопросы закрытого типа: «один из многих» и «многие из многих».
Вопросы этого типа предполагают, что необходимо вычислить правильный ответ и выбрать его из предложенного списка. Верных ответов может быть несколько. Если ответ требует округления, то округление производится по обычным правилам. Выбор правильного ответа осуществляется мышью. В примерах правильные ответы отмечены символом « ».
».
Пример 3. По списку в группе 20 студентов. Пусть X – число студентов, которые сдадут предстоящую сессию в срок. Какое из перечисленных событий является противоположным для события A = (X < 4)?
Ответы:  1) (X
1) (X  4);
4);  2) (X
2) (X  3);
3);  3) (X
3) (X  5).
5).
Пример 4. Число X выбирают наудачу из множества {1, 2, 3, 4, 5, 6}. Пусть событие A состоит в том, что число X делится на 3, а событие B – число X делится на 2. Укажите исходы этого эксперимента, составляющие событие A + B.
Ответы:  1) (X = 1);
1) (X = 1);  2) (X = 2);
2) (X = 2);  3) (X = 3);
3) (X = 3);
 4) (X = 4);
4) (X = 4);  5) (X = 5);
5) (X = 5);  6) (X = 6).
6) (X = 6).
3. Вопрос на установление соответствия: «множественное соответствие».
Вопросы этого типа содержат два списка разной длины. Первый список – это перечень характеристик, которые требуется определить, а второй – возможные значения этих характеристик.
Пример 5. Стрелок попадает в цель с вероятностью 0,9. Пусть случайная величина X равна числу пробоин в мишени при двух выстрелах. Укажите значения вероятностей в соответствующих клетках таблицы:
| 0,01 | 0,10 | 0,18 | 0,81 | 0,90 | ||
| P (X =0) = | ||||||
| P (X =1) = | ||||||
| P (X =2) = | ||||||
| P (X =3) = |
Так должна выглядеть таблица верных ответов. Клетки таблицы выбираются мышью.
| 0,01 | 0,10 | 0,18 | 0,81 | 0,90 | ||
| P (X =0) = | V | |||||
| P (X =1) = | V | |||||
| P (X =2) = | V | |||||
| P (X =3) = | V |






