Выполнение задания 1 следует начать с определения категории и сингонии, к которой принадлежит данная точечная группа. Это необходимо для выбора кристаллографической системы координат. Поскольку, в формуле 
содержится более одной оси симметрии выше второго порядка, определяем, что заданная группа относится к высшей категории, в которой имеется всего одна сингония - кубическая.
Для начала определим систему координат, свойственную данной сингонии, к которой принадлежит заданная точечная группа, и строим ее проекцию на плоскость 
. Затем, в соответствии с правилами записи международного символа точечной группы, строим проекции элементов симметрии, входящих в символ.
|
Рис. 1
На первом месте в данной сингонии стоит координатный элемент симметрии. Это инверсионная ось симметрии четвертого порядка, которая совпадает с координатной осью 
и изображается в виде одиночного незалитого квадратика в центре координат 
. На втором месте в формуле находится ось симметрии третьего порядка, которая в кубической сингонии всегда совпадает с пространственной диагональю куба, т.е. составляет со всеми координатными осями одинаковые углы. На нашей схеме она изобразится в виде треугольника со штрихом, лежащего на диагонали, между осями 
и 
, на которую проецируется пространственная диагональ куба. И, наконец, последний элемент является диагональным. Если это ось, то она совпадает с диагональю между осями и 
, а если плоскость, как в нашем случае, то она располагается перпендикулярно этой диагонали.
Теперь, когда на рисунке наглядно представлено взаимное расположение формульных элементов симметрии, можно применять теоремы о сочетании элементов симметрии (теоремы сложения).
Теорема 1 о пересечении двух плоскостей пока неприменима из-за отсутствия пересекающихся плоскостей. Обратные теоремы желательно не рассматривать до тех пор, пока не проанализировано действие всех прямых. Согласно теореме 2 о пересечении двух осей, через точку пересечения осе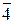й 
и 
должна проходить еще, как минимум, одна ось. Вокруг оси 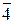должно располагаться четыре наклонных оси порядка , а через ось , в свою очередь, должно проходить три наклонных к ней оси .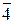
Рис. 2
Условия теорем 3, о пересечении четной оси симметрии и плоскости зеркального отражения, и 4, об осях симметрии второго порядка, перпендикулярных оси симметрии высшего порядка тоже пока отсутствуют на нашей схеме.
По теореме 5, если через ось симметрии 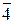проходит плоскость, то их должно быть только две, и они должны пересекаться под углом 
. Тогда должна быть еще одна плоскость, проходящая через ось .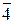
Рис. 3
Обратите внимание, что инверсионная ось четвертого порядка эквивалентна обычной оси симметрии второго порядка. Поэтому чрез неё проходит только две плоскости симметрии, а не четыре, как через обычную ось.
Проходящая через наклонную ось плоскость симметрии «даст» две дополнительных плоскости, проходящих через эту же ось под углом 
друг к другу. Эти плоскости пересекают боковые противоположные грани куба по их диагоналям, и они наклонены к плоскости проекции.
Теперь, в случае наклонных плоскостей, инверсионная ось четвертого порядка окружена уже не двумя, а четырьмя плоскостями, что соответствует порядку оси. Но эти плоскости попарно наклонены в разные стороны, что обусловлено инверсионным характером оси. Это отражено на рисунке с помощью знаков “+” и “-“.
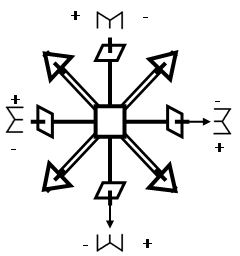Рис. 4
После того, как применены все теоремы, необходимо убедиться, что ничего не упущено. Для этого повторно проверим условия всех теорем.
Условия теоремы 1 теперь встречаются, но ничего не добавляют, т.к. на всех линиях пересечения плоскостей уже лежат оси симметрии. Теорема 2 так же реализована полностью, потому что нет точек пересечения, через которые проходит только две оси симметрии.
Условия для действия теорем 3 и 4 по-прежнему не появились. Поскольку через все оси проходят плоскости симметрии в количестве равном порядку оси, то и теорема 5 нами полностью учтена. Пересчитав все появившиеся элементы симметрии, запишем формулу точечной группы: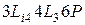 
.
