Параболой (рис.1) называется геометрическое место точек, равноудалённых от заданной точки F, называемой фокусом параболы, и данной прямой, не проходящей через эту точку и называемой директрисой параболы.

Уравнение параболы (рис.1):
y 2 = 2 p x.
Здесь ось ОХ является осью симметрии параболы.
Пусть Р (х 1, у 1) – точка параболы, тогда уравнение касательной к параболе в данной точке имеет вид:
у 1 y = p (x + х 1).
Условие касания прямой y = m x + k и параболы y 2 = 2 p x:
2 m k = p.
Понятия алгебраической операции, группоида, полугруппы и группы.
Определение алгебраической операции. Соответствие, в силу которого каждой паре a, b элементов множества M, взятых в данном порядке, соответствует единственный третий элемент с того же множества M, называется алгебраической операцией, определенной в M.
Г руппоид (тоже самое что и магма, только термин группоид старше) - множество с одной бинарной операцией 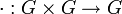 , обычно называемой умножением. Помимо требования замкнутости множества относительно заданной на нём операции, других требований к операции и множеству не предъявляется.
, обычно называемой умножением. Помимо требования замкнутости множества относительно заданной на нём операции, других требований к операции и множеству не предъявляется.
Полугруппой называется всякое множество с заданной на нем бинарной ассоциативной операцией. Или это группоид с ассоциативной операцией. Пример: Положительные целые числа с операцией сложения. Любая группа является также и полугруппой.
Структура: Если  , то принято обозначать
, то принято обозначать 
Группа — непустое множество с определённой на нём бинарной операцией, удовлетворяющей указанным ниже аксиомам.
Примерами групп являются действительные числа с операцией сложения, множество вращений плоскости вокруг начала координат и т. п.
Определения. Непустое множество 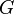 с заданной на нём бинарной операцией
с заданной на нём бинарной операцией  называется группой
называется группой  , если выполнены следующие аксиомы:
, если выполнены следующие аксиомы:
1. ассоциативность:  ;
;
2. наличие нейтрального элемента:  ;
;
3. наличие обратного элемента: 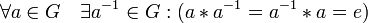
32. Определение кольца и поля. Простейшие свойства колец и полей.
Определение кольца
Кольцом  называется множество элементов, на котором определены две операции – сложение и умножение, и в
называется множество элементов, на котором определены две операции – сложение и умножение, и в  выполняются следующие аксиомы:
выполняются следующие аксиомы:
- R.1. Множество
 является аддитивной абелевой группой.
является аддитивной абелевой группой. - R.2. Для любых двух элементов
 и
и 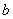 из
из  определено их произведение:
определено их произведение:  (замкнутость операции умножения).
(замкнутость операции умножения). - R.3. Для любых трех элементов
 ,
, 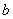 и
и  из
из  выполняется ассоциативный закон, т.е.
выполняется ассоциативный закон, т.е.  и
и  .
. - R.4. Для любых трех элементов
 ,
, 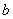 и
и  из
из  выполняется дистрибутивный закон, т.е. справедливы равенства:
выполняется дистрибутивный закон, т.е. справедливы равенства:  и
и  .
.
Определение поля
Полем  называют коммутативное кольцо с единицей, в котором каждый ненулевой элемент имеет мультипликативный обратный элемент (т.е. обратный по умножению).
называют коммутативное кольцо с единицей, в котором каждый ненулевой элемент имеет мультипликативный обратный элемент (т.е. обратный по умножению).
Другими словами, полем называют множество, которое является аддитивной абелевой группой; ненулевые же элементы этого множества образуют мультипликативную абелевую группу, и выполняется закон дистрибутивности.
По аналогии с группами число элементов поля называется порядком поля. Поля, порядки которых конечны, называются конечными полями. Конечные поля имеют наибольшее значение в теории кодирования.
Отметим некоторые свойства полей, вытекающие из их определения.
1. Для любого элемента поля  .
.
2. Для ненулевых элементов  и
и 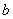 поля
поля  .
.
3. Для любых элементов  и
и 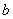 поля
поля  .
.
4. Если 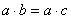 и
и  , то
, то  .
.






