 |
Геометричний зміст методу Ньютона полягає в тому (рис. 11), що дуга кривої
замінюється дотичною до цієї кривої (звідси і друга назва: метод дотичних).
Припустимо, що відділенням коренів знайдено початкове наближення х 0 до кореню. В точці х 0 розраховують ліву частину розв’язуваного рівняння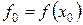 
, а також похідну в цій точці 
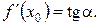Наступне наближення до кореню знайдемо в точці х 1, де дотична до функції 
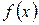, що проведена із точки 
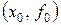, перетинає вісь абсцис. Отриману точку х 1 приймають за начальну і продовжують далі ітераційний процес. З рис. 11 видно, що таким способом можна наближатися до кореню х *. При цьому з кожною ітерацією відстань між черговим xn +1 і попереднім xn наближеннями до кореню буде зменшуватися. Процес уточнення кореню закінчується, коли виконується умова
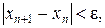
де ε – допустима похибка визначення кореню.
З геометричних співвідношень (див. рис. 11) отримують основну формулу методу Ньютона
У загальному вигляді для n -го кроку ітераційного процесу це співвідношення запишеться наступним чином
Отже, на кожному кроці ітерації відбувається заміна графіка функції дотичною до нього.
Методу Ньютона притаманна висока швидкість збіжності ітераційного процесу (достатньо 5 – 6 ітерацій для досягнення абсолютної точності рішення 10–5 – 10–6.
Недоліком методу Ньютона є необхідність розрахунку на кожній ітерації не тільки лівої частини рівняння, але й її похідної.
Можна, дещо знизивши швидкість збіжності, обмежитися розрахунком похідної 
тільки на першій ітерації, а потім обчислювати лише значення 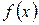, не змінюючи похідну . Цей алгоритм називають модифікованим методом Ньютона
 |
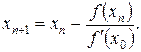
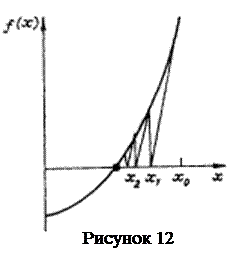Геометричний зміст модифікованого методу Ньютона продемонстровано на рис. 12.
Метод Ньютона можна застосовувати для уточнення коренів в області комплексних значень х, що необхідно при розв’язанні багатьох прикладних задач.
Метод січних
У методі Ньютона треба розраховувати похідну функції, що не завжди зручно. Якщо ітерації xn і xn +1 розташовані достатньо близько одна до одної, то похідну 
в алгоритмі Ньютона можна замінити її наближеним значенням у вигляді відношення приросту функції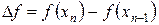 
і приросту аргументу 
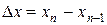. Отже, можна записати формулу методу січних
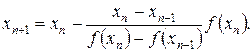
Для того щоб почати ітераційний процес, необхідно задати два початкових наближення х 0 і х 1. Потім кожне нове наближення до кореню отримують за вище написаною формулою. Процес уточнення кореню закінчується при виконанні умови
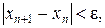
де ε – задана абсолютна похибка визначення кореню.
Ітераційні процеси, в яких для розрахунку чергового наближення потрібно знати два попередніх, називають двокроковими. Ця, нібито, невелика зміна в алгоритмі сильно впливає на характер ітерацій, тому метод січних дещо уступає методу Ньютона в швидкості збіжності, але він не вимагає обчислення похідної лівої частини рівняння.
 |
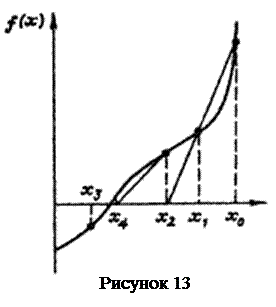Зазначимо, що геометричний зміст змін, внесених до алгоритму Ньютона, полягає в тому, що від апроксимації функції
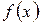дотичною зроблено перехід до січної (рис. 13).
За алгоритмом метод січних близький до алгоритму методу хорд, але на відміну від методу хорд початкові наближення в методі січних можуть розташовуватися як з різних боків від кореню, так і з одного боку; крім того, при уточненні кореню не повторюються знаки функції .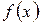
Метод простих ітерацій
Замінимо рівняння 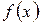рівносильним рівнянням 
. Цього можна досягти багатьма способами, наприклад, поклавши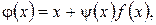 
де 
– довільна неперервна знакопостійна функція.
Нехай ξ – корінь цього рівняння, а х 0 – отримане якимось способом нульове наближення до кореню ξ. Підставимо х 0 в праву частину записаного вище рівняння, отримаємо деяке число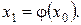 
Виконаємо те ж саме з х 1, отримаємо 
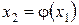і т. д. Застосовуючи крок за кроком співвідношення 
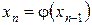для n = 1, 2, …, утворюємо числову послідовність х 0, х 1, …, хn, яку називають послідовністю наближень або ітераційною послідовністю.
 |
Процес побудови ітераційної послідовності має просту геометричну інтерпретацію (рис. 14).
Якщо ітераційна послідовність збігається, а функція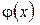 
неперервна, то ліміт послідовності є шуканим коренем рівняння.
