РАЗДЕЛ 4. ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Теория массового обслуживания – это математическая теория, ставящая целью изучение систем массового обслуживания (СМО).
Теория массового обслуживания начала развиваться в начале XX столетия.
Основоположником теории массового обслуживания считается датский ученый Агнер Краруп Эрланг. В 1909 г. Эрланг применил теорию вероятностей к исследованию зависимости обслуживания телефонных вызовов от числа поступивших на телефонную станцию вызовов.
Значительный вклад в создание и разработку общей теории массового обслуживания внес выдающийся советский математик Александр Яковлевич Хинчин (1984 – 1959). Он предложил сам термин теория массового обслуживания и систематизировал основные положения теории системы массового обслуживания в монографии «Работы по математической теории массового обслуживания» (М.: Физматгиз, 1963).
В зарубежной литературе теория массового обслуживания известна под названием «Теория очередей».
Предметом изучения теории массового обслуживания являются СМО - системы, предназначенные для многоразового использования при выполнении однотипных задач.
Цель теории массового обслуживания – выработка рекомендаций по рациональному построению СМО, рациональной организации их работы и регулированию потока заявок для обеспечения высокой эффективности функционирования СМО.
Для достижения этой цели ставятся задачи теории массового обслуживания, состоящие в установлении зависимостей эффективности функционирования СМО от ее организации (параметров): характера потока заявок, числа каналов и их производительности и правил работы СМО.
В сфере производства и обслуживания примерами СМО могут служить: различные системы связи (в том числе телефонные станции), погрузочно-разгрузочные комплексы (порты, товарные станции), автозаправочные станции, пункты пропуска через границу, пункты таможенного оформления, парикмахерские, билетные кассы, пункты обмена валюты, ремонтные мастерские, больницы и т.д. Такие системы как компьютерные сети, системы сбора, хранения и обработки информации, транспортные системы, автоматизированные производственные участки и, в военной области, системы противовоздушной или противоракетной обороны также могут рассматриваться как своеобразные СМО.
Глава 8. ПОТОКИ СОБЫТИЙ. КЛАССИФИКАЦИЯ СМО.
Случайные процессы и потоки событий.
В качестве аппарата теории систем массового обслуживания используют понятия теории случайных величин, а также теории случайных процессов.
Определение. Случайным процессом, или случайной функцией S(t), называется функция, которая каждому моменту времени t; из некоторого временного промежутка ставит в соответствие единственную случайную величину S(t).
Определение. Если состояния системы S изменяются во времени случайным образом, то будем говорить, что в системе S протекает случайный процесс.
По множеству состояний системы S протекающий в ней случайный процесс может быть дискретным или непрерывным. В дальнейшем мы будем иметь дело с дискретными случайными процессами. Тогда система переходит от состояния к состоянию скачком (в непрерывных процессах состояния системы меняются постепенно и плавно). Будем полагать, что в каждый момент времени система может находиться только в одном из своих состояний.
Определение. Случайный процесс, протекающий в системе S, называется марковским, если обладает свойством отсутствия последействия, или отсутствия памяти, т.е. для любого фиксированного момента времени t0 вероятность состояния в будущем (при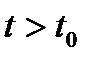 
) зависит только от состояния системы в настоящем (при 
) и не зависит от того, как развивался этот процесс в прошлом (при 
).
Определение. Потоком называется последовательность событий, наступающих одно за другим, в общем случае, в случайные моменты времени.
Определение. События в потоке называются однородными, если они различаются только по моментам времени их наступления, и неоднородными в противном случае.
В дальнейшем будем рассматривать только потоки однородных событий, не оговаривая это специально.
Определение. Поток событий называется потоком без последействия, или потоком без памяти, если для любой пары непересекающихся промежутков времени число событий за один из этих промежутков не зависят от числа событий за другой.
Очевидно, что регулярный поток событий, в котором события наступают через строго определенные промежутки времени, не обладает свойством отсутствия последействия, поскольку регулярность этого потока порождает последействие.
Определение. Поток событий называется ординарным, если вероятность наступления за достаточно малый (элементарный) промежуток времени более одного события пренебрежимо мала по сравнению с вероятностью наступления одного события за этот промежуток.
Определение. Поток событий называется стационарным, если вероятность наступления какого-либо числа событий за некоторый промежуток времени зависит только от длины этого промежутка и не зависит от момента его начала.
Очевидно, что вероятностные характеристики стационарного потока не зависят от времени, что и отражено в названии этого потока.
Определение. Простейшим (пуассоновским) называется поток событий, который обладает свойствами стационарности, отсутствия последействия и ординарности.
Определение. Интенсивностью потока 
называют среднее число событий, которые появляются в единицу времени.
Теорема 8.1. Если постоянная интенсивность потока известна, то вероятность появления m событий простейшего потока за время длительностью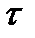 
определяется формулой Пуассона
. (8.1)
Эта теорема является основополагающей для теории систем массового обслуживания.
Формула (8.1) отражает все свойства простейшего потока.
Действительно, из формулы видно, что вероятность появления m событий за время 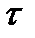, при заданной интенсивности является функцией m и 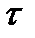, что характеризует свойство стационарности.
Формула не использует информации о появлении событий до начала рассматриваемого промежутка, что характеризует свойство отсутствия последействия. Легко можно убедиться, что формула отражает свойство ординарности.
Итак, формулу Пуассона можно считать математической моделью простейшего потока событий.
Пример 8.1. На автоматическую телефонную станцию поступает простейший поток вызовов с интенсивностью λ =1,2 вызовов в минуту. Найти вероятность того, что за две минуты:
а) не придет ни одного вызова;
б) придет ровно один вызов;
в) придет хотя бы один вызов.
Решение.
а) Случайная величина X – число вызовов за две минуты – распределена
по закону Пуассона с параметром λτ =1,2 ∙ 2 = 2,4. Вероятность того, что вызовов не будет (m = 0), по формуле (8.1):
.
б) Вероятность одного вызова (m = 1) по формуле (8.1):
.
в) Вероятность хотя бы одного вызова:
.
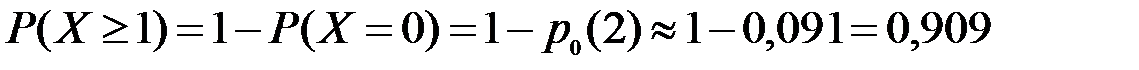