Рис. 5.5
|
Принципиальная электрическая схема представлена рис. 5.4; на рис. 5.5 показана схема расположения приборов и ручек управления на лицевой панели установки: 1 – тумблер включения установки; 2 – микроамперметр для измерения тока через термопару; 3 – цифровой омметр Щ4313 для измерения сопротивления, 4 – кнопка включения нагревателя; 5 – переключатель исследуемого образца, Rп/п, Rме – образцы из полупроводника и металла, 6 – нагреватель, Т – термопара.
Порядок выполнения работы
1. Ознакомьтесь с установкой.
2. Подготовить цифровой омметр Щ4313 к измерениям: на нем должны быть нажаты кнопки "сеть", "кW", "2", остальные отжаты, а входные штекеры вставлены в гнезда "*" и "U, кW".
3. Включите измерительные приборы, дайте им прогреться.
4. Подготовьте таблицу по форме 5.2.
5. Измерьте и запишите комнатную температуру T к.
6. Нажмите один раз кнопку нагрева 4 (кнопку нажатой не держать!).
7. Измерьте значения сопротивления полупроводника (переключатель 5 в положение "п/п") и металла (переключатель 5 в положение "мет." ) при значениях тока I от минимального до 800 мA через каждые 100 мA (см.табл.5.2).
Внимание! Не допускайте перегрева образцов. Для этого отключить нагреватель, нажав кнопку нагрева 4 сразу после измерений при токе 800 мА; при этом температура какое-то время будет ещё повышаться.
8. Повторите измерения аналогично п.7 в процессе охлаждения образцов при токе термопары 800 мА, 700 мА и так далее.
9. Вычислите среднее значение всех сопротивлений Rп/п и Rмет, полученных при нагревании (п.7) и охлаждении (п.8) образцов по формуле:
Rср=(Rнагр+Rохл)/2.
10. Используя градуировочный график (рис.5.6), определить температуру образца Т по значению силы тока в цепи термопары.
11. Результаты измерений и вычислений занести в таблицу по форме 5.2.
Таблица 5.2.
| Нагрев | Охлаждение | Среднее | Т, К |  ,
.10-3 К-1
| 
| ||||
| I, 10-6А | Rп/п, 103 Ом | Rме, 103 Ом | Rп/п, 103 Ом | Rме, 103 Ом | Rп/п, 103 Ом | Rме, 103 Ом | |||
| T к= | |||||||||
12. После окончания измерений выключите приборы и источники питания.
13. Постройте графики зависимостей R м= f (Т), R п/пр= f (Т) и ln R п/пр= f (1/T).
14. По графику R м= f (Т) определите температурный коэффициент сопротивления для металла a, для чего найдите по графику R0 – сопротивление металла при Т=273 К, и по формуле (5.9) найдите a по некоторому значению RМ и соответствующей ему температуры t 0C.
15. По формуле (5.1) найдите концентрацию электронов в металле, воспользовавшись табличными данными: D м=8600 кг/м3; μ= 0.064 кг / моль; z Cu=1. Вычислите для металла r, g и u n из формул (5.7), (5.6) и (5.5) соответственно, если l / S = 0.1 м -1.
16. Используя график зависимости ln R п/пр= f (1/T), определитеширину запрещенной зоны полупроводника e g по формуле (5.19). Выразите e g в джоулях и в электрон-вольтах.
17. Все полученные данные запишите в табл.5.3.
Таблица 5.3
| R0, Ом | α, К-1 | n, м-3 | ρ, Ом.м | g, Ом-1м-1 | un, м2с-1В-1 | e g, Дж | e g, эВ |
Контрольные вопросы
1. Чем определяется различие проводимости металлов, диэлектриков и полупроводников? От каких величин зависит удельная электропроводимость?
2. Что такое подвижность?
3. Объясните механизм возникновения сопротивления металла.
4. Как зависит сопротивление металла от температуры и почему?
5. Дайте определение температурного коэффициента сопротивления. В каких единицах он измеряется?
6. Как объясняет зонная теория деление твердых тел на металлы, полупроводники и диэлектрики?
7. Что такое валентная зона? Зона проводимости? Запрещенная зона? Как они образуются?
8. Сформулируйте принцип Паули.
9. Выведите формулу (5.17).
10. Объясните механизм собственной проводимости в полупроводниках.
11. Как зависит сопротивление полупроводника от температуры и почему?
12. Что такое энергия активации?
13. Объясните методику определения ширины запрещенной зоны (энергии активации) полупроводника.
Используемая литература
[1] §§ 43.1, 43.2, 43.3, 43.4, 43.5;
[2] §§ 13.11, 40.1, 40.2, 40.3, 40.6;
[3] §§ 4.42, 4.43, 4.45, 4.46, 4.48, 4.49, 4.50, 4.51, 4.52;
[4] т.2, § 34;
[5] §§ 98, 238, 240, 241, 242, 243.
Лабораторная работа 2-06
Изучение процессов заряда и разряда конденсатора (ФПЭ-08)
Цель работы: изучение заряда и разряда конденсатора при различных параметрах емкости и сопротивления электрической цепи и вычисление времени релаксации.
Теоретическое введение
Рассмотрим процесс заряда конденсатора в электрической цепи, содержащей последовательно соединенные конденсатор С, сопротивление R и источник ЭДС ε (рис. 6.1). Первоначально конденсатор не заряжен. Пусть I, q, U – мгновенные значения тока, заряда и разности потенциалов между обкладками конденсатора. Полагаем, что токи и напряжения удовлетворяют условиям квазистационарности, т.е. мгновенное значение тока во всех сечениях провода и элементах цепи (рис. 6.1) одно и то же, и соотношение между мгновенными значениями I, q и U такое же, как и в цепи постоянного тока. В момент времени t =0 ключ К замкнули, и в цепи пошел ток, заряжающий конденсатор 
, где q – заряд конденсатора. Применим закон Ома к цепи (рис. 6.1):
, (6.1)
где R – полное сопротивление цепи, включающее внутреннее сопротивление источника ЭДС. Учитывая, что разность потенциалов на пластинах конденсатора U = q / C, запишем предыдущее уравнение в виде
, (6.2)
Разделим переменные и проинтегрируем это уравнение с учетом начального условия: при t =0, q =0:
;
;
Откуда
, (6.3)
|
 |
Напряжение на конденсаторе изменяется по закону
,
закон изменения тока в цепи получим дифференцированием:
, (6.4)
где 
. Графики зависимостей q (t) и I (t) представлены на рис. 6.2.
Рассмотрим процесс разряда конденсатора емкостью С, пластины которого замкнуты сопротивлением R. Пусть dq – уменьшение заряда конденсатора за время dt. При разряде конденсатора в цепи (рис. 6.3) протекает ток 
. Известно, что 
, где U – разность потенциалов на конденсаторе, а следовательно, и на сопротивлении R. По закону Ома имеем U = IR, тогда
, (6.5)
Уравнение (6.5) показывает, что скорость уменьшения заряда конденсатора пропорциональна величине этого заряда. Интегрируя уравнение (6.5) при условии, что в момент времени t =0 q = q 0, получим
,
, (6.6)
откуда
, (6.7)
Функция q (t) называется экспоненциальной. График зависимости q (t) приведен на рис. 6.4. Закон изменения напряжения на конденсаторе в процессе разряда аналогичен (6.7):
, (6.8)
где 
. Произведение RС имеет размерность времени (
) и называется постоянной времени, или временем релаксации 
. За время заряд конденсатора уменьшается в e раз. Для определения RС часто удобно измерять время, за которое величина заряда падает до половины первоначального значения, так называемое "половинное время" t 1/2. "Половинное время" определяется из выражения
, (6.9)
Взяв натуральный логарифм от обеих частей уравнения (6.9), получаем 
, или
(6.10)
Способ измерения постоянной времени состоит в определении t 1/2 и умножении полученной величины на 1.44. Так как экспонента асимптотически приближается к оси абсцисс, то точно установить окончание процесса разряда конденсатора (так же как и процесса заряда) не представляется возможным. Поэтому целесообразно измерять время уменьшения величины заряда в 2 раза, т.е. “половинное время”. За каждый интервал времени t1/2=0.693ּ RC заряд на емкости уменьшается в два раза (рис. 6.5).
Кроме того, постоянную времени можно найти графическим способом. Из формулы (6.8) находим:
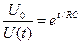, (6.11)
Логарифмируя левую и правую части формулы (6.11), получаем
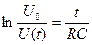. (6.12)
Построив логарифмическую зависимость, y = f (x), где 
, а 
, получим прямую, котангенс угла наклона которой к оси Х есть характеристическое время релаксации заряда, или постоянная времени RC:
. (6.13)
Если обкладки конденсатора попеременно подключать к источнику тока и к сопротивлению R (рис. 6.6), то график процесса заряд-разряд конденсатора будет иметь вид, показанный на рис. 6.7. Процесс заряда-разряда можно наблюдать с помощью осциллографа, подавая на вход Y напряжение с конденсатора C.
Экспериментальная часть
Приборы и оборудование: ФПЭ-08 (ПИ) – модуль “Заряд-разряд конденсатора”; ИП – источник питания; PQ – звуковой генератор; МС – магазин сопротивлений (R 1); МС – магазин сопротивлений (R 2); МЕ – магазин емкостей (С); РО – электронный осциллограф.
Функциональная схема лабораторной установки представлена на рис.6.8.
Методика измерений
Схема состоит из источника постоянного тока ИП, генератора низкочастотных синусоидальных импульсов (звукового генератора), преобразователя ПИ синусоидальных импульсов в прямоугольные 
положительной полярности (преобразователь импульсов позволяет получить прямоугольные импульсы, скважность которых меняется регулятором на лицевой панели), двух магазинов сопротивлений R 1 и R 2, магазина емкостей С и электронного осциллографа.
Подаваемый с выхода генератора синусоидальный импульс преобразуется в прямоугольный и через магазин сопротивлений R 2 подается на магазин емкостей С. Конденсатор заряжается. Время заряда конденсатора С можно изменять сопротивлением R 2. В момент паузы происходит разряд конденсатора по цепи R 1– R 2– C. Время разряда определяется параметрами этой цепи.
Визуально процесс заряда-разряда конденсатора можно наблюдать на экране осциллографа. Наиболее устойчивый режим работы данной схемы обеспечивается при изменении номинальных величин элементов RC –цепи в следующих пределах:
С=0.02÷0.04 мкФ; R1=102÷103 Ом; R2=1÷5 кОм; fген=0.5÷5 кГц.
При этом сравнительно полно происходит процесс заряда-разряда конденсатора. При увеличении сопротивлений и емкости больше определенных значений конденсатор не успевает полностью зарядиться и разрядиться за один период цикла. Наблюдаемые при этом кривые заряда и разряда изображены на
 |
рис.6.9 штрихпунктирной линией.
Порядок выполнения работы
1. Ознакомиться с работой звукового генератора и электронного осциллографа.
2. Установить следующие параметры выходного напряжения звукового генератора: частота 2 кГц, напряжение 2-3 В.
3. Установить импульсы наибольшей скважности. Для этого нажать левую кнопку “скважность–грубо” преобразователя импульсов ПИ (модуль ФПЭ-08). Ручку “скважность–точно” установить в крайнее правое положение.
4. Подготовить осциллограф к работе:
а) установить ручку развертки «время/дел» в положение «50 μs»;
б) ручку усилителя «вольт/дел» установить в положение «1 V».
5. Включить лабораторный стенд и приборы: источник питания, генератор, осциллограф.
6. Установить на экране осциллографа устойчивую картину.
7. Установить на магазине сопротивлений R 1 значение 1.102 Ом.
8. Установить на магазине сопротивлений R 2 значение 2.103 Ом.
9. Установить на магазине емкостей значение С =2ּ10-2 мкФ.
Задание 1: Изучение кривых заряда и разряда конденсатора.
1. Установить усиление канала Y осциллографа таким, чтобы высота импульса на экране была максимальной. Ручками «↔» и «↕» осциллографа совместить начало кривой заряда с началом шкалы осциллографа. Установить частоту развертки осциллографа такой, чтобы на экране уместилась полная кривая заряда и разряда конденсатора. Снять кривую зависимости Y = f (X), измеряя X в секундах, а Y – в вольтах. Записать 8-10 значений X и Y. Результаты занести в таблицу 6.1, построить кривую заряда конденсатора U=f (t).
Таблица 6.1.
| Процесс заряда; R 1=1.102 Ом; R 2=…..Ом; С =….. мкФ. Цена деления по оси Х: 50 μs/дел. | ||||||||||
| X, дел. | ||||||||||
| X, c | ||||||||||
| Y, В |
2. Аналогичные измерения провести для кривой разряда, совместив начало кривой разряда с началом координат на шкале осциллографа. Результаты занести в таблицу 6.2, построить кривую разряда конденсатора.
Таблица 6.2
| Процесс разряда; R 1=1.102 Ом; R 2=…..Ом; С =….. мкФ. Цена деления по оси Х, 50 μs/дел. | ||||||||||
| X, c | ||||||||||
| Y, В | U 0= | |||||||||
|
3. По кривым заряда и разряда конденсатора определить время, за которое величина напряжения падает до половины первоначального значения (“половинное время”) и по формуле 6.10. вычислить время релаксации 
.
4. Не изменяя усиление канала Y осциллографа, получить на экране кривые заряда и разряда конденсатора при других значениях R 2 и С, оставляя неизменной величину сопротивления R 1=102 Ом.
Рекомендуемые значения R 2 и С следующие:
R 2=1.103 Ом; C =2×10-2÷4×10-2 мкФ;
R 2=2×103 Ом; C =1×10-2 мкФ;
R 2=3×103 Ом; C =1×10-2 мкФ.
5. Измерить по наблюдаемым на экране осциллографа кривым релаксации заряда “половинное время” в делениях шкалы. Затем t 1/2 перевести в секунды. По формуле (6.10):
(6.10)
вычислить экспериментальное значение постоянной времени τ эксп.. (Для получения достаточно полного процесса заряда и разряда конденсатора можно изменять частоту следования импульсов, меняя частоту звукового генератора.)
7. Вычислить теоретическое значение постоянной времени τтеор.= RC, используя значение параметров RC – цепи. Учесть, что при заряде конденсатора R = R 2, а при разряде R = R 1+ R 2.
8. Вычислить относительную погрешность Е (τ) постоянной времени в каждом опыте по формуле (6.11); рассчитать среднюю.
. (6.14)
9. Данные занести в таблицу 6.3.
Таблица 6.3
| R 2, ּ103 Ом | C, ּ10-2 мкФ | t 1/2, с | R, Ом | τ эксп., с | τтеор, с | Е (τ), % | Е среднее |
Задание 2: Построение кривой разряда конденсатора в логарифмическом масштабе
1. Рассчитать значения 
, записать в табл.6.2.
2. Построить график зависимости Y = f (X), где 
, а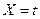 
(рис.6.10).
3. Найти котангенс угла наклона полученной прямой к оси Х как отношение:
.
4. Сравнить полученное значение 
со значением постоянной времени, найденным в задании 1: 
.
5. Записать результаты в табл.6.4.
Таблица 6.4.
| R 1, 103 Ом | R 2, 103 Ом | C, 10-2 мкФ | R, Ом | Δt, с | Δ
|  ,с
| τтеор, с |
Контрольные вопросы
1. Что такое кривая релаксации заряда?
2. Как определяется характеристическое время релаксации τ?
3. Опишите блок-схему установки.
4. Как зависит время заряда и разряда конденсатора от элементов цепи R1, R2, C?
5. Какова зависимость напряжения на конденсаторе U и тока в цепи I от времени, т.е. U (t) и I (t), в процессе заряда и разряда конденсатора?
6. Вывести формулы (6.3) и (6.7).
Используемая литература
[2] § 13.8;
[3] §§ 2.32, 3.14;
[4] т.2, §§ 80, 81, 82.
Лабораторная работа 2-07
Изучение релаксационных колебаний (ФПЭ-12)
Цель работы: снятие вольт–амперной характеристики газонаполненной лампы и изучение релаксационных колебаний.
Теоретическое введение
Релаксационные колебания – незатухающие негармонические колебания нелинейных систем, для которых характерно накопление и сбрасывание энергии (relaxation – ослабление). Их генератором может служить система «газонаполненная лампа-конденсатор» (рис.7.1).
 |
При подключении генератора к источнику e начальное сопротивление незажженной лампы велико, конденсатор С заряжается, одновременно растет разность потенциалов на электродах газонаполненной лампы.
Газы в естественном состоянии состоят из электрически нейтральных атомов и молекул, т.е. не содержат свободных зарядов и поэтому не проводят электрический ток. Проводить они могут, только если часть молекул ионизируется – расщепляется на положительные и отрицательные ионы. Обычно происходит расщепление на одновалентный положительно заряженный ион и электрон. Ионизация может происходить под влиянием различных воздействий на газ, например, нагрева, космических лучей, бомбардировки молекул газа быстро движущимися ионами и электронами (ударная ионизация) и др. (Заметим, что наряду с процессом ионизации в газе происходит и обратный процесс – рекомбинация, т.е. воссоединение положительных и отрицательных ионов в нейтральный атом.)
Так как в обычных условиях газ всегда подвергается действию космических лучей и радиоактивных излучений, то в нем всегда имеются свободные заряды. Однако интенсивность ионизации Δ n i, измеряемая числом пар ионов равного знака, возникающих в единице объема газа в единицу времени, в обычных условиях очень мала и не может обеспечить существенной электропроводности. Поэтому газы ведут себя как изоляторы. Наряду с процессом ионизации в газе происходит и обратный процесс – рекомбинация, т.е. воссоединение положительных и отрицательных ионов в нейтральные атомы. Вероятность такого процесса пропорциональна как числу положительных, так и числу отрицательных ионов. Поэтому количество рекомбинирующих за 1 с в единице объема пар ионов Δ n r пропорционально квадрату имеющихся в единице объема пар ионов:
, (7.1)
где k – коэффициент рекомбинации.
Под влиянием ионизации и рекомбинации в газе устанавливается равновесное состояние (так называемое динамическое равновесие), когда число пар ионов, возникающих в единичном объеме в единицу времени, равно числу рекомбинирующих пар: 
. В состоянии равновесия в единице объема газа будет находиться n пар ионов:
(7.2)
Если газ, находящийся под действием внешнего ионизатора, заключен в колбу с впаянными в нее электродами (“лампа”), то при подаче на электроды напряжения через газ потечет ток, который называют газовым разрядом. В этом случае электропроводность газа создается за счет внешнего ионизатора, и ток, возникающий в нем, называется несамостоятельным разрядом. С прекращением действия внешнего ионизатора такой разряд прекращается.
Электрический ток в газе, сохраняющийся после прекращения действия внешнего ионизатора, называется самостоятельным газовым разрядом. Для его осуществления необходимо, чтобы в результате самого разряда в газе непрерывно образовывались свободные заряды.
Плотность электрического тока в газе j (электрический ток, проходящий через единицу площади поперечного сечения) обусловлена движением как положительных, так и отрицательных зарядов:
, (7.3)
где q + и q – – величины положительных и отрицательных зарядов; 
и 
– средние квадратичные скорости упорядоченного движения зарядов; n – концентрация зарядов.
Средние скорости упорядоченного движения пропорциональны напряженности электрического поля Е:
; (7.4)
. (7.4а)
где 
и 
– подвижности положительных и отрицательных зарядов (скорости их упорядоченного движения при напряженности электрического поля Е =1 В/м).
Тогда
. (7.5)
Сравним эту формулу с законом Ома в дифференциальной форме:
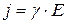; (7.6)
где γ – электропроводность (электропроводимость; проводимость).
Электропроводность будет равна:
. (7.7)
Учитывая, что газы ионизируются, как правило, на электрон и одновалентный положительно заряженный ион, можно записать:
. (7.8)
Зависимость тока от приложенного к электродам напряжения называется вольтамперной характеристикой. Она изображена на рис. 7.2. Если к электродам приложить напряжение, то ионы и электроны под действием сил со стороны электрического поля будут двигаться к противоположным электродам. При малых напряжениях (участок 1) концентрация зарядов остается постоянной, так как интенсивность ионизации 
будет постоянной, а электродов будет достигать лишь незначительное число заряженных частиц. Поэтому электропроводность также остается постоянной, а сила тока пропорциональна напряженности электрического поля в соответствии с законом Ома (7.6).
С увеличением разности потенциалов (участок 2) линейная зависимость нарушается. Это связано с тем, что под действием электрического поля значительная часть ионов и электронов достигает электродов. Начиная с некоторого значения напряжения (участок 3) ток остается неизменным с увеличением напряжения (I н – ток насыщения). Это объясняется тем, что все заряды, возникшие в газе под действием внешнего ионизатора, достигают электродов лампы, не успевая рекомбинировать. Поэтому при неизменной интенсивности ионизации не происходит дальнейшего роста тока при увеличении напряжения. Если в объеме трубки V в единицу времени образуется 
пар свободных зарядов и все они приходят на электроды, то ток в трубке будет:
(7.9)
где I н – ток насыщения – максимально возможный ток при данной интенсивности ионизации. Газовый разряд, происходящий на участках 1, 2 и 3 является несамостоятельным газовым разрядом.
При дальнейшем увеличении напряжения (участок 4) происходит резкое увеличение тока. Это объясняется ударной ионизацией: электроны, возникшие в газе за счет внешнего ионизатора, во время своего движения к аноду под действием электрического поля приобретают энергию, достаточную для ионизации нейтральных молекул газа при столкновении с ними. При столкновении образуются вторичные электроны и ионы. В свою очередь вторичные электроны, ускоряясь полем, могут также ионизировать нейтральные молекулы газа.
Число носителей тока лавинообразно возрастает, возрастает и величина тока. Но разряд в газе остается еще несамостоятельным, так как ударная ионизация, вызванная одними электронами, недостаточна для поддержания разряда при удалении внешнего ионизатора. Это вызвано тем, что электроны движутся в электрическом поле от катода к аноду. Поэтому они могут ионизировать только те молекулы газа, которые лежат ближе к аноду по сравнению с местом возникновения данного электрона. Вблизи катода электроны еще не имеют энергии, достаточной для ионизации, и в этой области электроны могут возникать только благодаря внешнему ионизатору.
Если действие ионизатора прекратится, то область ударной ионизации будет постепенно сокращаться, стягиваясь к аноду по мере движения к нему электронов, и в конце концов ударная ионизация и электрический ток в газе прекратятся. Переход от несамостоятельного разряда к самостоятельному становится возможным лишь при таком напряжении между электродами, когда положительные ионы также приобретают энергию, достаточную для ионизации молекул газа, т.е. возникают два встречных потока, каждый из которых способен вызвать ионизацию газа. В этом случае внешний ионизатор не играет существенной роли в осуществлении газового разряда, так как число создаваемых им первоначальных ионов мало по сравнению с числом вторичных ионов, и прекращение действия ионизатора не влияет на протекание разряда.
Опыт показывает, что в большинстве случаев наблюдается не ударная ионизация молекул газа ионами, а выбивание ими электронов с поверхности катода, так как в этом случае работа, совершаемая ионом, меньше, чем при ударной ионизации. Наряду с процессом выбивания ионами электронов из катода – вторичной эмиссией, не менее важным является фотоэффект – выбивание электронов из катода под действием света: достаточно быстрый электрон может не только ионизировать молекулу, но и перевести образовавшийся ион в возбужденное состояние. Переходя затем в устойчивое состояние, ион испускает квант энергии, который способен вызвать фотоионизацию. Испускание света происходит при рекомбинации положительных ионов с электронами – “рекомбинационное свечение”.
Повышая напряжение на электродах, можно возбудить все эти процессы и осуществить переход от несамостоятельного разряда к самостоятельному. Этот переход называется электрическим пробоем газа, а соответствующее напряжение – напряжением зажигания (U з). Оно зависит от химической природы газа, материала катода, формы электродов и расстояния между ними, давления газа и наличия в нем примесей.
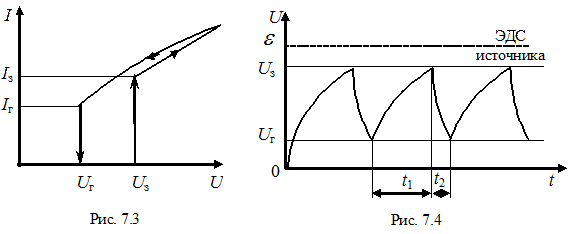
Идеализированная вольтамперная характеристика газонаполненной лампы приведена на рис.7.3. При напряжении U < U з токи в лампе при обычных внешних ионизаторах малы, и мы их рассматривать не будем
Если увеличивать разность потенциалов на электродах лампы, то при значении U = U з скачком устанавливается значение тока, равное I з – лампа “загорается”. При дальнейшем возрастании напряжения ток растет по закону, близкому к линейному.
|
Если затем уменьшать напряжение на “горящей” лампе, то при напряжении, равном U з, лампа еще не гаснет. Продолжая уменьшать напряжение, можно увидеть, что лишь при некотором напряжении – напряжении гашения U г, которое меньше, чем U з, лампа “гаснет” и ток скачком резко падает. На этом самостоятельный разряд в лампе прекращается. При дальнейшем возрастании напряжения процесс повторяется. Следует заметить, что для реальной лампы зависимость I = f (U) не является линейной, причем при U > U з кривые, снятые при возрастании и убывании напряжения, не вполне совпадают. Но эти отличия несущественны, и мы можем ими в данной работе пренебречь.
Газонаполненные лампы часто используют для получения релаксационных колебаний. Релаксационные колебания – периодические колебания, по форме резко отличающиеся от синусоидальных и представляющие собой периодически повторяющийся процесс возрастания электрического напряжения и последующего его уменьшения.
Рассмотрим работу генератора релаксационных колебаний. Принципиальная схема представлена на рис. 7.1. Он состоит из источника, дающего постоянное напряжение U 0, конденсатора емкостью С, сопротивления R и лампы Л. Если включить источник, то в цепи появится ток. Сопротивление незажженной лампы бесконечно велико, и ток I ЗАР будет заряжать конденсатор. Разность потенциалов на его обкладках будет расти. Соответственно растет и разность потенциалов на электродах лампы, подсоединенной параллельно конденсатору. Когда она достигнет значения напряжения зажигания U з, лампа “зажжется” – ее сопротивление R Л скачком уменьшится, и она начнет проводить ток. Так как R>>R Л, то ток разряда конденсатора потечет через лампу. Это вызовет быстрое падение напряжения на конденсаторе, и когда оно достигнет значения напряжения гашения U г, лампа “гаснет”, и процесс начинается сначала. Возникают релаксационные колебания. Кривая изменения напряжения на конденсаторе представлена на рис. 7.4 и представляет собой негармонические релаксационные колебания. Наблюдая эти колебания на экране осциллографа, можно рассчитать их период: 
; здесь t 1 – время накопления энергии, t 2 – время сброса.
Период релаксационных колебаний в генераторе лампа-конденсатор может быть также определен, если наблюдать на осциллографе фигуры Лиссажу (замкнутые линии, получающиеся при сложении двух взаимно перпендикулярных колебаний). Для этого на одну пару пластин осциллографа подается напряжение с генератора лампа-конденсатор, на другую – переменное напряжение известной частоты от звукового генератора.
Отношение частот колебаний можно определить по виду фигуры Лиссажу, оно равно отношению числа касаний фигуры с прямой, параллельной оси Х и с прямой, параллельной оси Y. На рис. 7.6 (стр.68) показан вид фигуры Лиссажу для соотношения частот 1:1.
Найдем закон, по которому будет меняться напряжение на конденсаторе.
В любой момент времени величина напряжения U 0 равна сумме напряжений в элементах цепи:
; (7.10)
где U – разность потенциалов на обкладках конденсатора.
Заряд конденсатора изменяется вследствие протекания по цепи электрического тока:
; (7.11)
изменение заряда вызывает изменение разности потенциалов:
. (7.12)
Из уравнений (7.11) и (7.12) находим:
. (7.13)
Подставляя (7.13) в (7.10) получаем:
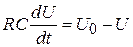. (7.14)
Преобразуем выражение (7.14):
(7.15)
и проведем интегрирование:
. (7.16)
Постоянная интегрирования находится из условия: при t =0 U =0: 
. Потенцируя выражение (7.16), получим закон возрастания напряжения на конденсаторе генератора релаксационных колебаний:
. (7.17)
Критическое значение энергии конденсатора
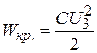. (7.18)
Экспериментальная часть
Приборы и оборудование: источник питания ИП; электронный осциллограф РО; звуковой генератор PQ; амперметр РА (Ф214/1); магазин сопротивлений МС; магазин емкостей МЕ; модуль ФПЭ-12.
Функциональная схема представлена на рисунке 7.5.
 |
|
|
В работе определяется период релаксационных колебаний двумя способами. Первый способ заключается в том, что сигнал от полученных в цепи релаксационных колебаний поступает на вход осциллографа и на экране последнего можно наблюдать изображение этих колебаний.
Период можно измерить непосредственно с экрана при работе осциллографа в режиме измерения длительности сигнала.
Второй способ, более точный, заключается в том, что дополнительно на второй вход осциллографа поступает сигнал определенной частоты. В электронно-лучевой трубке происходит сложение двух взаимно перпендикулярных колебаний: релаксационных колебаний лампы и синусоидальных колебаний, подаваемых на второй вход осциллографа. В результате на экране появятся фигуры Лиссажу. Если частоты складываемых колебаний относятся как целые числа, то картина на экране неподвижна. Зная частоту подаваемого сигнала, по виду фигуры Лиссажу можно определить соотношение частот и частоту релаксационных колебаний. В отличие от сложных гармонических колебаний фигура Лиссажу при соотношении частот 1:1 не имеет вид эллипса (рис. 7.6).
